 Newton's
equations work just as well backwards as forwards.
Newton's
equations work just as well backwards as forwards.
Incorporate answers to reading questions into class
 Newton's
equations work just as well backwards as forwards.
Newton's
equations work just as well backwards as forwards.
(very little friction): In the middle, can you tell if the movie of these pendulums is being run forwards or backwards?
(lotsa friction) What about this silly one?
...and yet, even the one that you can tell is shot backwards doesn't violate any laws of physics that we know about so far:
Why couldn't a bunch of water molecules in a lake all of a sudden find themselves moving in the same direction, so as to eject the human swimmer?? And yet we know this rarely ~ never happens.
Coin-flipping exercise
If you are fascinated by the meaning of entropy, read The Library of Babel--a short story by Jorge Luis Borges.
The law of heating is one way of stating the second law...
Thermal energy flows spontaneously from higher to lower temperature, but not from lower to higher temperature.
What does that mean for our hot rock and cold water situation?
A lot of modern engines work like this:
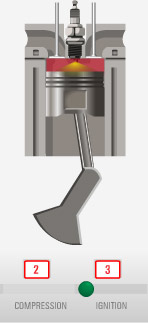 Many modern machines use heat to make some sort of mechanical motion
happen. In a gas engine...
Many modern machines use heat to make some sort of mechanical motion
happen. In a gas engine...
In a nuclear-powered  submarine,
submarine,
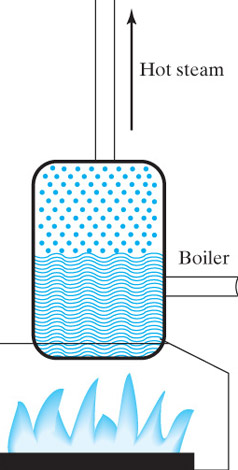
You can use the steam to push a rod back and forth (howstuffworks.com) to power a steam locomotive,
or more commonly:
 The expanding steam pushes against the blades of a turbine to make a shaft
turn,
The expanding steam pushes against the blades of a turbine to make a shaft
turn,
If you attach the shaft to magnets, and rotate them past electric coils you can cause a current to flow--*electricity*.
A heat engine is a device that uses thermal energy in some form, converting some of it into mechanical energy (KineticE) in a cyclic process.
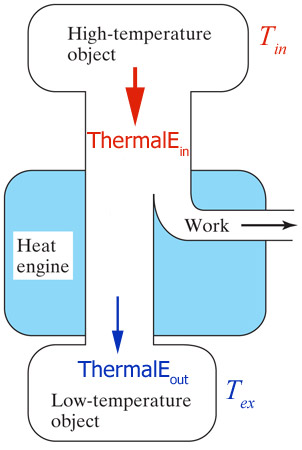 Just
like any other energy transformation, a portion of the input energy goes to...ThermalE.
Just
like any other energy transformation, a portion of the input energy goes to...ThermalE.
What's the efficiency of the cartoon heat engine shown?
energy efficiency = $\frac{W o r k_{out}}{ThermalE_{i n}}$
Example - A certain steam engine gets 50 kWh of heat from burning coal, and performs 12 kWh of mechanical work. What is its efficiency?
efficiency = 12 kWh / 50 kWh = 0.24 = 24%
The law of heat engines is another way of stating the second law...
Any cyclic process that uses thermal energy to do work must also have a thermal energy exhaust: Heat engines are always less than 100% efficient at using thermal energy to do work.
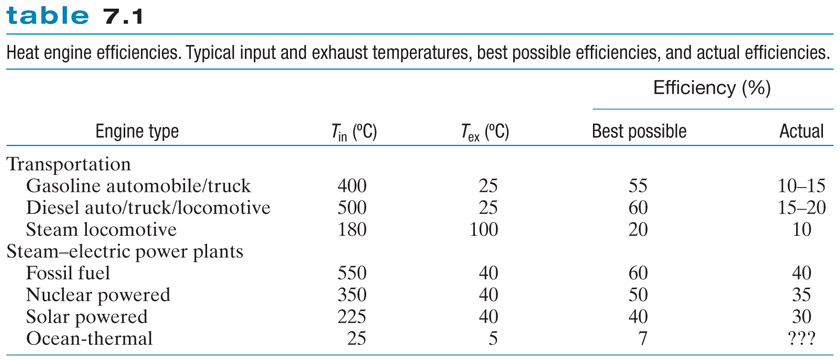
There is a pattern to be found here, for how the efficiency depends on $T_{in}$ and $T_{exhaust}$. Stare at the table, and see if you can see it...
$$\text{ efficiency}_{max} =\frac{T_{Hot}-T_{Cold}}{T_{Hot}}= 1-T_{Cold}/T_{Hot} .$$
So the theoretical best (e.g. no engine friction...) you could do with a gasoline engine is... $$eff = 1-T_{cold}/T_{hot}=1-298/673=0.557 = 56\%.$$
So...how could you change a gas engine to be more efficient (and thus save lots of energy!)??
Efficiency of an engine with high temp of 500 C: $$1-298/773=.614$$
These days...
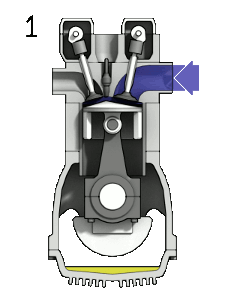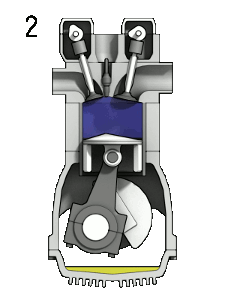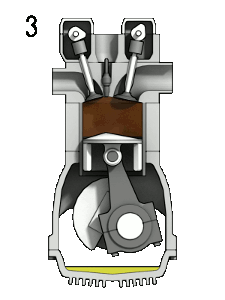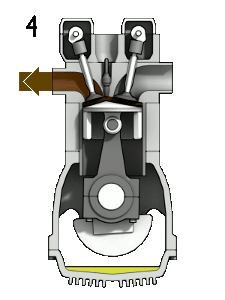 Gas engines: Fuel and gas are compressed, and then ignited with a spark
plug.
Gas engines: Fuel and gas are compressed, and then ignited with a spark
plug.
When you compress a gas it gets hotter. Problem: pre-ignition, so, you'd better not go above the temperature for spontaneous ignition
 Diesel
engines: No spark plug. Air is compressed to a greater pressure than
in a gas engine, get's way hot, then diesel is sprayed in and ignites spontaneously.
Diesel
engines: No spark plug. Air is compressed to a greater pressure than
in a gas engine, get's way hot, then diesel is sprayed in and ignites spontaneously.
Gas in the UK currently costs ~2.5 $\times$ U.S. gasoline (> $7 / gallon)
35-50% of passenger cars sold in Europe are diesels.
Should you always avoid the lowest efficiency heat engines? Must the exhausted heat *always* be wasted?
Look up "co-generation"...
Possible downsides of diesel engines??
Thermal energy has a lower "quality" in this sense:
All other energy forms $\rightarrow$ ThermalE: Easy to convert 100% to ThermalE.
ThermalE $\rightarrow$ any other energy form: Efficiency is often pretty low (much less than 100%) .
 DC electric motors can have efficiencies of more than 95%.
DC electric motors can have efficiencies of more than 95%.
 If the human body were a heat engine, what would its efficiency be??
If the human body were a heat engine, what would its efficiency be??
Take $T_{in}$ = body temperature = 98.6 F = 310.15 K, and $T_{ex}$ = atmospheric temp = 70 F = 294.3 K$
The efficiency of a heat engine operating between those two temperatures would be... $$\frac{T_{hot}-T_{cold}}{T_{hot}} = \frac{T_{310}-T_{294}}{T_{310}} = 0.052 \approx 5.2\%$$
But we know its actual efficiency is closer to 25%.
This means our bodies are much more amazing than internal combustion engines (as if you didn't already know...): Our muscles are converting chemical energy directly to mechanical energy, without going through a stage where the chemical energy is turned into heat.
 What
happens to the organized, collective motion of a water drop once it hits?
What
happens to the organized, collective motion of a water drop once it hits?
 Consider two groups of 6 atoms.
Consider two groups of 6 atoms.
So, the total kinetic energy of each collection is the same: $6*\frac{1}{2}mv^2$.
The only way they differ is in their degree of disorganization = entropy.
a) - organized motion might be the atoms in a drop of water all moving the same direction, or a bunch of electrons (in an electric current) all moving in the same direction.
b) - disorganized motion: "thermal energy".
If you want to use the kinetic energy from a group of atoms to push a car to make it start going, or lift a bucket of water from a well... Would you rather start with a) or b)??
 A heat engine could be used to connect a hot container of molecules, and a
cool one and extract some work.
A heat engine could be used to connect a hot container of molecules, and a
cool one and extract some work.
After simulating mixing hot and cold molecules .... Is there any way to get work out of the mixture? With a higher or lower efficiency than if we had kept the hot and cold separate?
Entropy is a quantitative measure of a system's microscopic disorganization.
The total entropy of all the participants in any physical process cannot decrease during that process, but it can increase.
 [conceptual exercise #22]
[conceptual exercise #22]
A pan of water is set outside on a cold day.
Initially it is a liquid, but after a while, it freezes solid.
Molecules in a solid are more ordered than atoms in a liquid. So, is this a violation of the "Law of Entropy"?
[writing .... ]
As the water cools, heat escapes in the form of atoms. These atoms are very random, which goes along with entropy...?
Heat is mostly a flow of energy, not atoms: What happens is that
Some of the heat from the air would go into the water.
Well, no. On average the fast water molecules are losing energy, and the colder (slower) air molecules are gaining that energy.
The atoms in the water and air combine causing disorganization.
Well, no. Here it's mainly just energy that is exchanged between the pan of water and the environment. More slowly moving water molecules are more "organized" than faster moving ones.
But this change in temperature is not the only way for atomic systems to get disorganized. It is true that if you mix orange juice and pineapple juice, the resulting mixture, where orange molecules and pineapple molecules are evenly spread out in the juice pitcher is less organized that the separate juices that you started with.
Conceptual exercises in Chapter 7: 1, 4, 6, 9, 10, 11, 16, 19, 22