Household Power

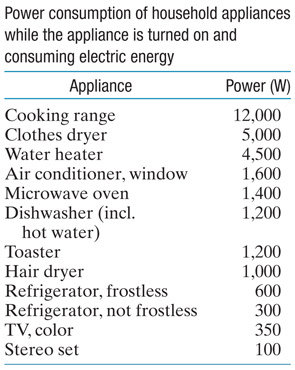
Well, actually power and energy 

Power at home

1,000 Watts = 1 kiloWatt (kW) = 1,000 J / s

Is the appliance that takes the most power the one that uses the most energy?

Since $\frac{E}{t} = P$

a little algebra $\Rightarrow$ $$ E = P \cdot t$$ So, for example, if an appliance draws power at a rate of 300 W = 300 J/s, and you run it for 50 seconds, then the energy used is...

$$300\frac{J}{s} * 50\,s = 15,000 J$$

so Power * time = energy. Which of these is a unit of energy? of power? neither?

kilowatts,     watts / hour,     kiloJoules,     milliJoules / day,     kilowatts * hours

Kilowatt$\cdot$hours ="kWh" is fairly commonly used--e.g. on electric bills.

How much energy do you use (in kWh):

• if you dry clothes for 1/2 hour?
• if you turn on an air conditioner for 10 hours?
• if you use a hair dryer for 6 minutes?
• How long could you listen to a your stereo (at full volume) before you used as much energy as drying your hair for 6 minutes?
• How much energy do you personally use if you and a friend have about the same amount of laundry and you throw it together and dry for half hour?
• Which uses more energy...Doing one 1/2 hour dryer run yourself once a week, or watching TV for 1 hour each day?

In many homes the refrigerator is the appliance that uses the most energy over the course of a year. (Eia.doe.gov)

David MacKay suggests that good units to use to think about your personal energy consumption are average energy used per day for one person: $$\frac{\text{kWh}}{\text{person}\cdot\text{day}}$$

To discuss in groups of 3-4: You have a device to measure instantaneous power consumption that tells you that when you're charging your laptop computer it draws 60 Watts of electrical power. What else would you need to know to estimate the average energy consumption of your computer in MacKay's suggested units? What if you don't charge it every day? Give some sample numbers and show the result.

Measuring your power usage

We've got two "KILL A WATT" meters that let you measure the electrical power usage of various appliances. To use the meter:

1. Plug the meter into the wall. A number close to 120 will show up on the screen. This is the AC voltage detected in your wall socket.
2. Press the middle button, labelled "Watt". The screen should show 0.
3. Plug something in to the plug on the front of the meter and turn it on. You should see its instantaneous power usage (in Watts).

To estimate how much power you use with a particular appliance:

1. Plug the appliance in to the meter, turn on the appliance, and note how much power it uses (in Watts).
2. Now, estimate how many minutes you use the appliance each day. Divide the number of minutes by 60 to get the number of (decimal) hours you use it in a day.
3. Multiply the power (Watts) by the time (hours) to calculate your usage in watt*hrs /day.

Appliances with rechargeable batteries, like laptop computers or cell phones, are a bit of a different case. If the battery is charging, you see one (higher) power reading. If the battery is already charged and it's plugged in, you'll see a different, lower power reading. To figure out the energy used, we will need to know how much energy it takes to charge the device to support all the time you use it for. The time you *use* your cellphone is not as important for this calculation as the time it takes to *charge* your cellphone. So, here's what to measure:

1. Measure the power used when the battery is charging (in Watts).
2. Estimate the total time you spend charging the device over the course of a week (in hours). If you have a laptop that is plugged in all the time, you'll have to unplug, run it down, and then see how long it takes to fully charge it up.
3. Then divide your weekly charging time by 7 to get your average daily charging time. Convert to hours from minutes if necessary.
4. Multiply your average daily charging time by the power to get a number (in Watt*hrs) for your average daily energy use for your rechargeable device.

Watts up

How much electricity does a typical household use?

U.S. Energy Information Administration figures for 2008 said we used 3.8 trillion kWh / year.

This works out to about ~30 kWh per day, per person.

This means that one person uses 30 kWh of *energy* in the course of one day. But power is energy / time, so that means a typical American consumes an average power of:

$$P=\frac{E}{time} = \frac{30kWh}{24 h}=1.25 kW.$$

So, 100 people would need a power station generating 125 kW on average.

Households: 107 million households used 1140 billion kWh/yr

This is about 10 kWh per day, per person: our home usage. The rest is our share of industrial/hospital/school/etc use.

Solar power

Could solar power meet our household needs?

Generating solar energy

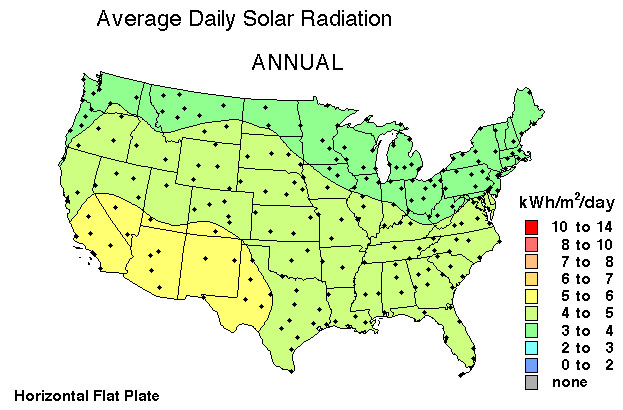
Typical family usage (Paul's!) ~$\frac{500 k W h}{m o n t h} \cdot \frac{1 m o n t h}{ 30 d a y s }$ ~17 kWh / day.

So, for 5 people, that's about 3-4 kW*hrs per day per person, the solar energy falling on 1 square meter of N. Indiana in an average day.

Current solar photovoltaic (PV) devices convert about 15% (~ 1/7) of the energy that falls on them into electricity. $=>$ we'd need about 7 square meters of solar panels per person.

Land use

Is 7 m${}^2$ / persons a ridiculous amount of land??

Compare this with the land area we as a society have dedicated to another public good: the interstate highway system. It's ~75,000 km long with an average density of 1000 km${}^2$ for every 800 km of length. That's an area of 94,000 square km. Dividing this by the current population of ~300 million, this works out to ~300 square meters of Interstate per person.

Daily variations

Both wind and solar are not *on* all the time, so some sort of supplementary storage is needed.

You can

• couple to hydroelectric dams, or
• pump water uphill (see Dinorwig)

Converting units

How many seconds / hour = "seconds per hour" = "seconds in each hour"?

There are 60 seconds in each minute: 60 s/ min.

There are 60 minutes in each hour: 60 min / hour.

"60 minutes in each hour, and 60 seconds in each of those minutes" = 60 min/hr $\times$ 60 sec/min = 3600 sec / hr = "3600 seconds in each hour".

Cost of electricity

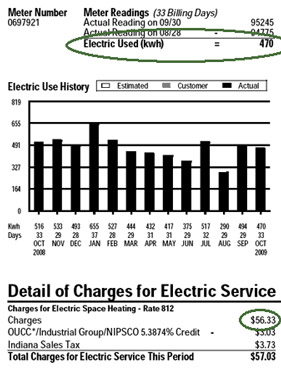We said $W=P \cdot t$

kwh=kilowatt hour= $10^3$ (J/s) $\cdot$ 1 hour $\times (3600 s)/(1 hr)= $ 3.6 million J

Cost of a 1 kwh of electricity: \$56.33 / 470 kwh = \$0.12 / 1 kwH

What would I pay for the ElectricE for the 5800 J needed to get one of you up three flights? More than a dollar? Less than a penny?

Cost table

Cost of food energy

What does a kWh worth of food calories cost?

[Writing]

Image credits

Tim Blaum, Elizabeth Albert