Work

...a connection between force and energy.

Some vague relationships:

Energy $\leftrightarrow$ 'damage' $\leftrightarrow$ change in environment

Does a force always cause a change in the environment??

Work

Forces?

When do forces cause a change in the environment?

• When a force is exerted an object,
• and the object moves.

Work = force $\times$ distance $= F \times d$

Work and Energy

Work is a transfer of energy.

Units?

• Measuring force in Newtons,
• distance in meters

$\Rightarrow$: 1 Newton $\cdot$ meter $\equiv$ 1 Joule $=2.78\times 10^{-4}$ Watt $\cdot$ hours $=2.39 \times 10^{-4}$ Calories.

Example: How much work?

How much work must you do to lift a 10N book (with a constant speed) up from the floor, to a point 2 m above the floor?

W = 10 N $\times$ 2m = 20 N$\cdot$m = 20 Joules.

Gravitational energy

Does a raised book have energy? Have the ability to cause destruction in its environment? How much destruction?

We think this gravitational energy depends on... mass $m$, height $h$, gravity's acceleration $g$.

Guess a formula for gravitational energy...

Gravitational energy

The answer is

$${\text GravE} = mgh$$

Notice that this is precisely how much work you need to do to lift the book when you pick it up directly:

$${\text Work}=F\cdot d =(mg)\cdot h$$

In the pulley lab, different pulley arrangements allowed you to lift with a different force. But the smaller the force $F$, the longer the distance you had to pull the string $d$.

If the lab went well, many of you found that

$$F\cdot d \approx mgh$$

The work you did on the weight was equal to the gravitational energy gained by the weight.

So the weight-on-a-string is like a gravitational battery:

• Lifting a book $\Rightarrow$ energy in.
• Dropping a book $\Rightarrow$ energy out.

Ability to do work

We say a system has energy if it has the ability to do work.

Energy of moving objects

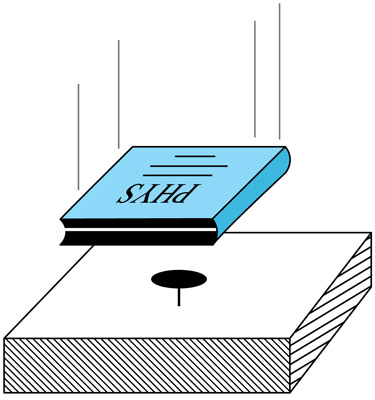
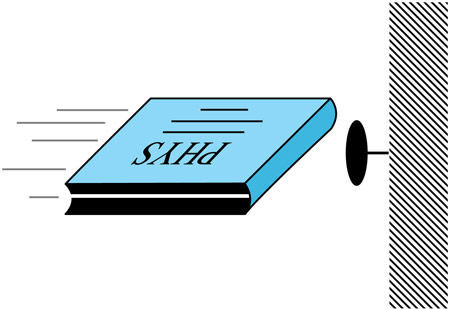It seems that moving objects also have the ability to do work.

How does energy depend on...

• mass $m$ of the moving object?
• speed $s$ of moving object?

Kinetic energy

The energy of a moving object is called kinetic energy and is equal to:

KineticE = $ \frac{1}{2}ms^2$

Many more lives are lost each year due to kinetic energy than due to nuclear energy!

Conversion of energy from one form to another

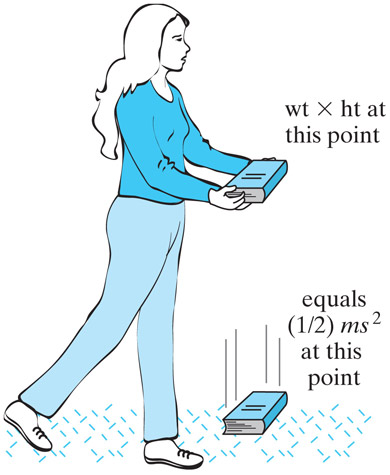An amazing observation... with no friction or air resistance, the gravitational energy of a book just before dropping turns out to be precisely equal to the kinetic energy of the book the instant before it hits the floor.

$$mgh =\frac{1}{2}ms^2$$

It is as if the gravitational energy was completely converted to kinetic energy.

This gives us a way of calculating how fast a dropped object is moving:

$$\begineq mgh &=& \frac{1}{2}ms^2\\ gh &=& \frac{1}{2}s^2\\ 2gh&=& s^2\\
\sqrt{2gh}&=&s\endeq$$

What is the speed of an object dropped from a height of 5 m (about 15 ft: the second story of the Ad building) just before it hits the sidewalk?

[Using $g \approx 10$ m/s^2, the number you get will have units of m/sec.]

How many miles per hour is that? Use WolframAlpha to find out...

Energy CONSERVATION

The more general way to think about this is to say

Energy is never lost--only converted from one form to another

We write it and understand it this way... that you have to add up all the possible forms of energy, and their sum is what never changes...

$$E_\text{ start} = E_\text{end}$$

$$GravE_{\text start}+KE_{\text start} = GravE_{\text end}+KE_{\text end}$$

$$mgh + 0 = 0 + \frac{1}{2}ms^2$$

$$mgh = \frac{1}{2}ms^2$$

Bring hotwheels car

Suggested exercises

Conceptual exercises, Chapter 6: 5, 6, 12, 15, 16