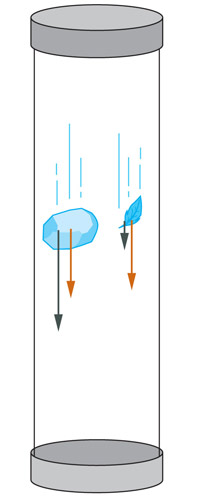
What might the arrows at left represent? Which of these are equal (not equal) for the feather and the rock?
But according to our equation for acceleration, $a=f/m$, a more massive object requires a bigger force to accelerate it at the same rate as a lighter object, no??
Yes, exactly! The force of gravity near the surface of the earth is called "weight"
$$W=mg$$
Since the weight is proportional to the mass of an object, this is exactly what is needed to produce the Law of Falling, so that all objects have the same acceleration.
A force results from an interaction between two bodies. If the earth pulls on a rock, isn't the rock pulling on the earth too?
So, it seems reasonable that the gravitational force $F_g$ is proportional to the masses of both bodies involved in the interaction. There's nothing so special about one or the other.
Newton's full equation for the gravitational force between two bodies of mass $m_1$ and $m_2$ does indeed depend on the masses of both:
With masses in kilograms and distances in meters:
$F_g = 6.7 \times 10^{-11}\frac{m_1 m_2}{d^2}$
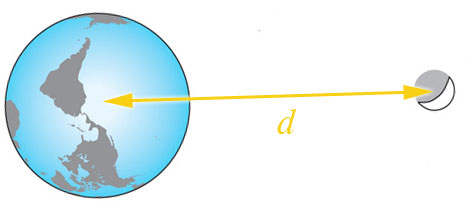
Distances from where to where? Surface to surface?
Distances are measured from the center of mass of one body to the center of mass of the other.
Materialism of Newton's day: A body can only exert a force on another body when the two are touching...
Sir Isaac Newton, 1642-1727
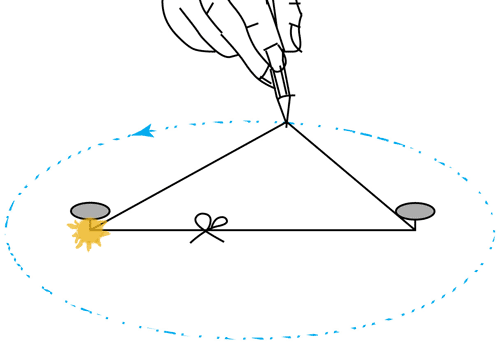Used calculus to show that his $F_g$ leads to elliptical orbits of the planets (confirming Kepler's observations).
With this force law and the just-invented calculus, Newton was able to show that planetary orbits around a massive body, like the sun, ought to be ellipses, just as Kepler had observed (but never explained).
Newton's equation for gravity means that the force of gravity at the surface of the earth on some object of mass $m$ is:
$$F_g \approx 6.7 \times 10^{-11} \frac{m_E \cdot m}{r_E^2} = 6.7 \times 10^{-11}\frac{5.97 \times 10^{24} {\rm kg}\cdot m}{(6.38 \times 10^6 m)^2} = 9.8 (m/sec^2) * m (kg)$$
Talk about how this changes even on the earth, but certainly on different planets.
According to the law of falling, all objects near Earth's surface fall (are accelerated at...) the same rate. That rate is called $g$, "the acceleration of gravity". $g=$
This
dragster accelerates from 0 to 100 mph in ~0.9 sec. 100 mph in one second ~
5 *(22 mph increase in one second) = 5g.
There is a formula for that relates distance and time (starting from rest) to acceleration. It is...
$$d = \frac{1}{2}at^2.$$
Solve it for $a$:
$$\frac{2 d}{t^2}= a.$$
World class sprinter:
40 m dash in 4.4 seconds:
$a = (2*40)/(4.4^2) \approx 4 $m / sec / sec = 0.4 * 10 m / sec / sec = 0.4 g.
John Stapp survived horizontal acceleration of $\approx 22g$ for more than a second (1954 USAF sled trial).
The human body can withstand only about $5g$ vertically before blood flow away from the head leaves you unconscious. The space shuttle is designed to limit accelerations to $3g$.
Conceptual Exercises in Chapter 5: 3, 4, 11, 12, 18, 22.
Problems in Chapter 5: 2, 3, 4