Why things move as they do

Aristotle thought a push (or force) was necessary to keep things moving.

But since Galileo...

A body subject to no external influences must maintain an unchanging velocity.

So, what do forces do?

One thing we know: you can measure force with some sort of spring scale.

bring spring scale, orange cart, track, spinny wheel on end, string

Demo first that weight is constant force, as measured by spring scale

Explain that weight is exerting a constant force on cart. What happens to velocity?? (changes) -> acceleration.
Start with 1 100g weight on cart, lightest weight on string.

Note what happens with greater weight -- explain that this is not changing the mass of the cart.

Note what happens with same weight, but change mass on cart...

Push cart against weight

A force causes velocity to change: causes acceleration.

acceleration = change in velocity / time

Units: (miles / hour) / hour or (meters / sec) / sec or meters / sec^2

A body subject to no forces must maintain an unchanging velocity.

One body exerts a force on another body whenever the first body causes the second body to accelerate.

Causes of unnatural motion

Pushes, pulls... Hammering on bowling ball. One magnet pulling a hunk of steel. Balloon attracting something else. A push or a pull by one body on another.

You can measure force with some sort of spring scale.

the Grammar of acceleration

What happens to the acceleration if we keep the body's mass the same, but increase the force on a body??

In words: Doubling the force causes the acceleration to double
or
"Acceleration is proportional to the force".

In math: $a \propto f$

In graphs:

What happens to the acceleration of a body, if we keep the force the same, but increase the mass of the body?

In words: Doubling the mass of an object cuts its acceleration in half
or
acceleration is inversely proportional to mass

In math: $a \propto 1/m$

In graphs:

Different objects have different 'resistance to acceleration': mass (units, kilograms - kg)

Putting these two patterns together

$a \propto f/m$

Units: if we measure:

mass in $kg$,
acceleration in $m/sec^2$,
force in Newtons (N) $=kg$ $m/sec^2$

$a = f/m$

"A force of 1 Newton accelerates a mass of 1 kg by 1 m per second in each second."

Concept Check #4

$a = f/m$

You push your 2 kg book along a tabletop, pushing it with a 10 N force. If the book is greased so that friction is negligible, the book's acceleration:

is 5 m/s²,
is 10 m/s²,
is 20 m/s²,
is 0.2 m/s²,
keeps getting larger and larger as long as you keep pushing,
keeps getting smaller and smaller as long as you keep pushing.

What keeps getting bigger as you push with a 10 N force??

Force has a direction

speedup

Multiple forces in action

Tug of war

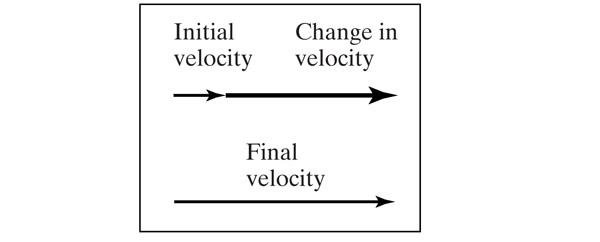
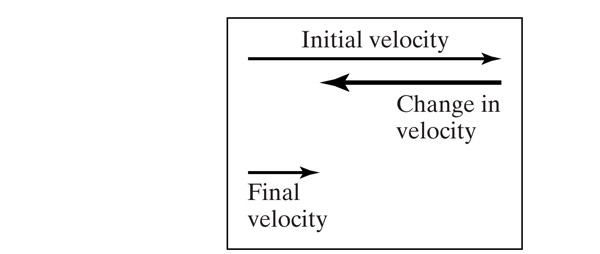
One body exerts a force on another body if, in the absence of other forces, the first body *would* cause the second body to accelerate.

Strick materialists (ca. Isaac Newton): The only way for one body to exert a force on another is if they are touching.

Bring stick--push against a student. Tell people to focus on the stick. Why no acceleration? Force...why no change in velocity???

The force $f$ in $a=f/m$ is apparently some sort of "net force" where you take into account the different directions of all the forces acting on a body. Some of the forces may cancel out other forces.

Bring stick--You and student pull each other without moving.

Suggested Exercises

Conceptual Exercises in Chapter 4: 2, 3, 5, 7, 8, 17.
Problems in Chapter 4: 1, 4, 8.

Image credits

Zunami