Leucippus
and his student Democritus (5th century BC) considered the possibility of
dividing a chunk of gold once, twice, many times and asked...
Leucippus
and his student Democritus (5th century BC) considered the possibility of
dividing a chunk of gold once, twice, many times and asked...
How long can this go on?
Either:
They found 1.) distasteful, so chose to believe that
$\Rightarrow$All matter is made of "atoms"; There is space (lots) between atoms.
[image: The young Rembrandt as Democritus the laughing philosopher]
What's the nature of the evidence that Democritus had for atoms? Do you buy it?
Leucippus and Democritus were strict materialists, who thought you should ask "What earlier circumstance lead to this event" vs.
"What purpose did this event serve?"
Here Krulwich wonders along these lines about Richard Feynmann at his wife's deathbed.
Before 1800 scientists realized that...
E.g. Pass electricity through water, and you can generate hydrogen and oxygen gas. But hydrogen and oxygen cannot be further decomposed.
In the early 1800s John Dalton (a Quaker) noticed that one kind of tin oxide could be decomposed into 13.5 grams of oxygen for every 100 g of tin. Another kind could be decomposed into 27 grams of oxygen for every 100 g of tin.
A simple integer ratio of 2:1. Is this evidence of atoms??
This could be explaind by atoms combining in definite ratios...
We now know the chemical formulae for the two tin oxides as SbO and SbO${}_2$.
Therefore we may conclude that the ultimate particles of all homogeneous bodies are perfectly alike in weight, figure, etc. In other words, every particle of water is like every other particle of water; every particle of hydrogen is like every other particle of hydrogen, etc.
Look at a table of the elements, and note the atomic weights of different elements. These have units of grams/"mole". E.g. hydrogen (~ 1 g/mole), carbon (atomic weight 12 g/mole) and oxygen (atomic weight 16 g/mole)...
This means one *atom* of carbon weighs 12 times what an atom of hydrogen weighs. What about Tin (Sb)?
Example of C and O reacting to form carbon monoxide, CO2
If oxygen and hydrogen combine into the compound H${}_2$O, then 1 pound of hydrogen would fully react with how many pounds of oxygen to form water?
Examples of what happens if you have equal weights of oxygen and hydrogen, say, one pound each. How much of what left over.
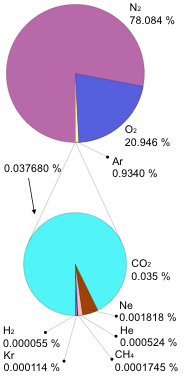Is mostly nitrogen
How many times heavier is a molecule of water than a nitrogen-gas molecule ($N_2$)?
What about air "heavy" with humidity?
Are atoms the only possible explanation for the patterns that Dalton observed?
Dalton thought that...
Atoms are, we think, moving all the time. You can't see it directly, but you can sometimes see things larger than atoms getting jostled by all this shaking.
This is called Brownian motion.
Einstein
made some calculations (1905) about how grains buffeted by random molecular
collisions would move which agreed well with experiment.
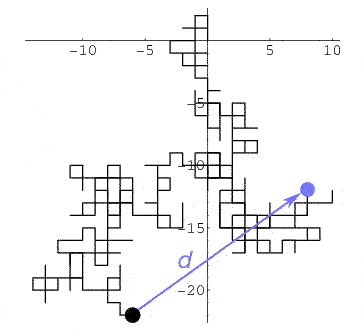
Look up random walk or drunkard's walk. [children's activity]
It can be shown that after he goes through $N$ intersections, he will on average be a distance $d\propto\sqrt{N}$ away from his starting point. [Though we have no idea of what direction away from his starting point he'll be.]
[image: Wolfram math world]
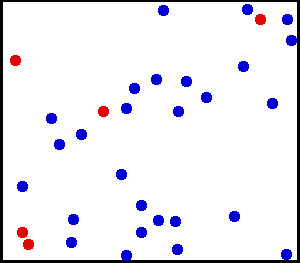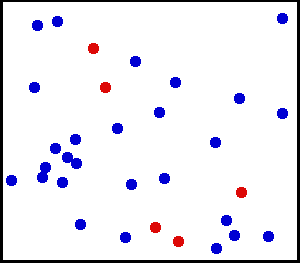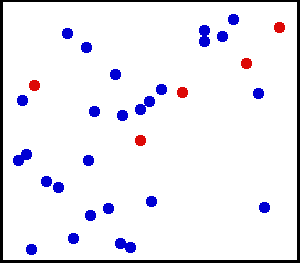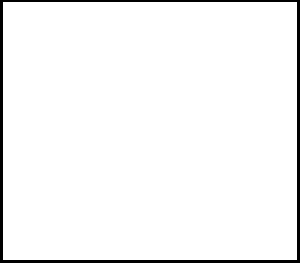Motion
of these atoms appears very random and disorganized. With each collision, the
speed and direction of each atom changes.
Is there anything that remains unchanging through all this change?
The average speed of a collection of many, many atoms changes very
slowly, despite all the collisions and changes at the atomic level.
Temperature is related to that average speed. When atoms go faster on average, the temperature increases.
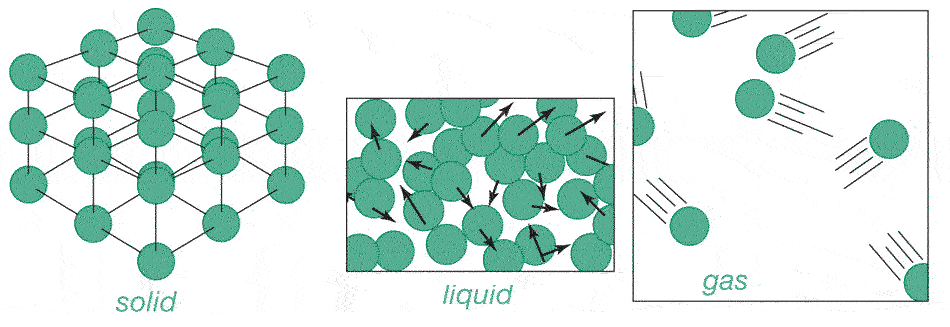
Heating things up causes the atoms to bounce against each other harder and harder, and a substance expands.
Going from a liquid to a gas, atoms move somewhat faster, but also take up much more space. e.g. Water:
Conceptual exercises in Chapter 2: 1, 2, 3, 5, 7, 13, 16, 21, 23, 28
Wikipedia - atmosphere, thermal motion
