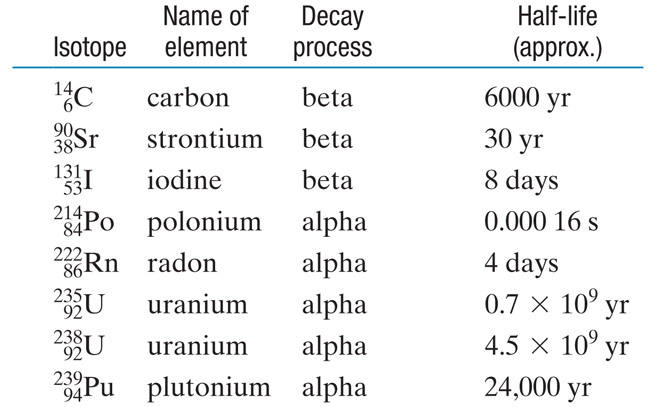
Throw 600 dice into the air all at the same time.
~ How many are likely to come down as 3?
Remove all the 3s.
Roughly 1/6 of dice come down as 3's each time. So, 100 the first time. If we remove these 100 we're left with 500. Roughly the number of dice we are left with after each throw:
| $N_{dice}$ | 1/6 of $N_{dice}$ | |
|---|---|---|
| 600 | 100 | |
| 500 | 83.3 | |
| 417 | 69.5 | |
| 347 | 57.8 | |
| 289 | .... |
Repeat....
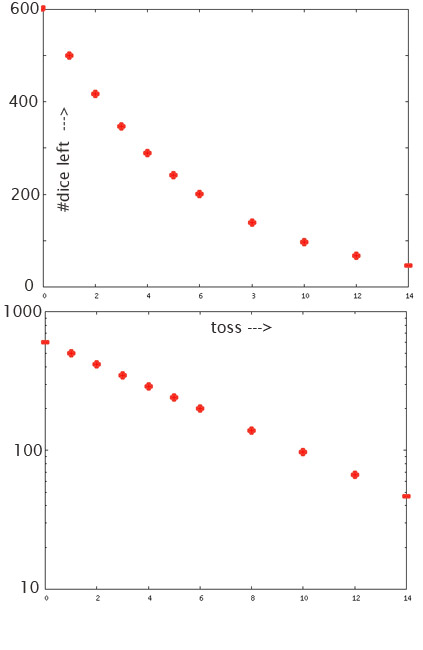
Dice-ish data:a "reversed J"-curve, straight on a semi-log plot, characterized by a half life.
Each dice has a characteristic probability that a "3" will be rolled in one toss: 1/6.
Each radioactive nucleus has a characteristic probability that it will decay in a second.
If the dice are tossed once per minute, what is the half-life for the number of dice: The time after which we have only half of the original number of dice?
Say you have 100 coins, and you throw them all up in the air once each minute, and then remove all the heads. What is the "half-life" for the number of coins left in minutes?
It is worth pausing to consider how weird this is:
The current world average lifespan at birth is 67.2 years.
If we died with a half-life of 67.2 years:
Humans seem to have a pretty firm "expires by" date, but not radioactive atoms.
Where do radioactive isotopes come from? We will find that many elements were made in stars.
There are 2 processes that affect ${}_6^{14}C$ in Earth's atmosphere. (Carbon in the atmosphere is mostly present in the chemical compound $CO_2$):
Eventually a balance is reached where the number that decay each year is ~ equal to the number of new ${}_6^{14}C$ nuclei produced each year.
This equilibrium ratio is about
1 ${}_6^{14}C$ : 1 trillion ($10^{12}$) ${}_6^{12}C$
Plants inhale ${}_6^{14}C$-containing
$CO_2$ while alive, and use this carbon to store sugars, build cell walls,
etc.
While alive, their ${}_6^{14}C$:${}_6^{12}C$ ratio is... the same as the atmosphere: ~ 1:trillion.
Death
means no new $CO_2$ coming in.
Carbon-14 decays to nitrogen, but no new ${}_6^{14}C$ is arriving.
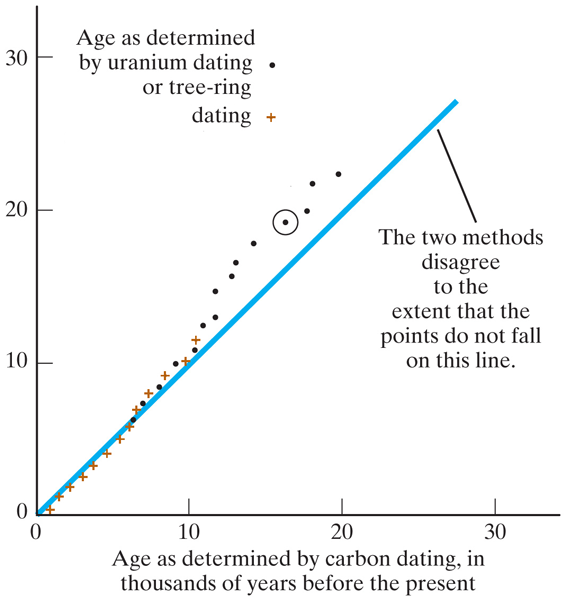
Grind up old leaves, and count the isotopes (in a mass spectrometer)...
| ${}_6^{14}C$ : ${}_6^{12}C$ ratio | Age (years) |
|---|---|
| 1.0 : 1 trillion 0.5 : 1 trillion 0.25 : 1 trillion 0.13 : 1 trillion |
0 6,000 12,000 18,000 |
The
U.S. Department of Alcohol, Tobacco, and Firearms tests alcoholic beverages
and will not allow it to be sold unless it has "enough"
radioactivity. Why?
There is a law in this country that alcoholic beverages may only be made from fresh fruits, and in particular not from petroleum products.
Petroleum is the remains of plant matter, but it has been underground for 10's or 100's of millions of years: Many, many half-lives of Carbon-14 (half-life=6000 years).
$\Rightarrow$ Petroleum will have virtually no Carbon-14, and therefore no Carbon-14 decays. So looking for radiation from Carbon-14 decays is an easy way to test for petroleum vs recent fruits.
All three naturally occuring oxygen isotopes are stable: ${}^{16}O$ (99.762% natural abundance), ${}^{17}O$,${}^{18}O$. So, assume no change in terrestrial isotope ratios.
Heavy water: $H_2O$ molecules with the heavier oxygen isotopes are heavier.
High
temps: at extremely high temps (boiling) all water molecules
go liquid $\rightarrow$ vapor.
Low temperatures: It's more likely for thermal jostling to kick a lighter $H_2O$ from liquid $\rightarrow$ vapor than a heavier one $\Rightarrow$
Chapter 14, Conceptual Exercises: 17, 19, 21, 34, 35
Oliver Kurmis, Ian Turk, Kurzon, Yzmo, Daniel Mayer, Peter Pick, water vapor, Torsten Reuschling
