Physics of Music 2007
On the Tuning of Oxygen Canister Bells
David Glick
Physics of Musics
Goshen College, Spring 2007
Introduction
Portable oxygen canisters of the sort used for medical purposes and by mountaineers and pilots are routinely discarded due to safety restrictions on their use. When the bottom of one of these is cut off and it is struck, it rings like a bell! Several artists have experimented with producing oxygen canister bells as artwork, but to my knowledge no one has investigated how their tuning might be adjusted precisely. At the behest of Russ Buschert, I decided to look into this with the hopes of facilitating the reuse of some of these discarded canisters through the construction of a playable sculpture.
Three approaches were considered in the attempt to create a range in pitch of at least an octave:
1. adjusting the thickness of the canister
2. changing the length of the canister
3. cutting slits on opposite sides of the canister
Finite Element Analysis and Calculix
The main technique that was used to investigate these changes was a finite element analysis using the open-source software package Calculix. Finite element analysis breaks an object into a mesh of small pieces and then analyzes their interactions by solving a huge system of simultaneous equations in order to determine the normal modes of vibration. A Perl script was used to run the Calculix simulations with various parameters for the length of the canister and the length of the slit; these were then compared to a few measurements made after modifications to an actual oxygen canister in order to confirm the reliability of the model. The modeling does not indicate which modes will be strongest or last the longest when the bell is struck at a particular location, so recordings of the bell being struck were also made to provide this additional information.
Adjusting canister thickness
Adjusting the thickness of the canister by turning it on a lathe was the first tuning method considered. This is how the oxygen canisters’ more musical cousin, the handbell, is tuned after casting. However, it was quickly determined that the canisters were not perfectly round enough for this to work well. Even if the canister could be handled properly on the lathe, the metal would be removed non-uniformly which would end up splitting the pitch of “twin” modes that would otherwise be practically degenerate.
Changing the length of the canister
The effect of shortening the cylinder was investigated after chopping through the steel canister with a pivoting band saw. The particular canister that was used had an initial length of 34cm, diameter of 10cm, and wall thickness of 2.5mm.
Ten centimeters were removed, with the result of lowering the pitch only a fraction of a semitone. As the following graph shows, this matches the prediction of the computer FEA model.
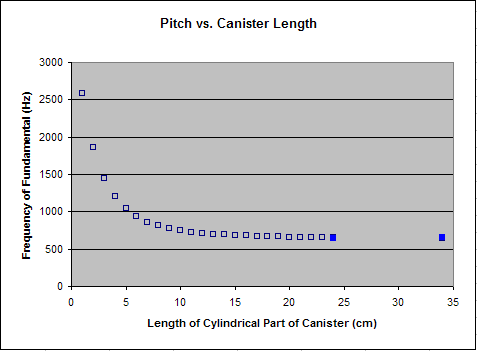
Based on the computer model, it appears that the pitch would not be significantly affected until the cylinder is made much shorter (less than about 10cm). Further cuts could be made on the canister to confirm this. However, since our purpose is to create a strikable sculpture and this would leave little area to strike, this solution was viewed as non-ideal.
Cutting slits in the canister
The final tuning technique that was investigated was cutting slits on opposite sides of the canister. It was hoped that this would allow additional vibration in a mode similar to that of a tuning fork, allowing for a lower pitch.
The computer model of adding this slit showed success in producing a continual decrease in pitch over the range of a couple octaves, and this prediction matched the experimental result. The disadvantage to this technique is that the addition of slits creates a nonuniformity which causes a considerable separation between the pitches of the bottom two vibrational modes. (Higher modes are also affected, but they have a much weaker contribution to the sound that is heard.)
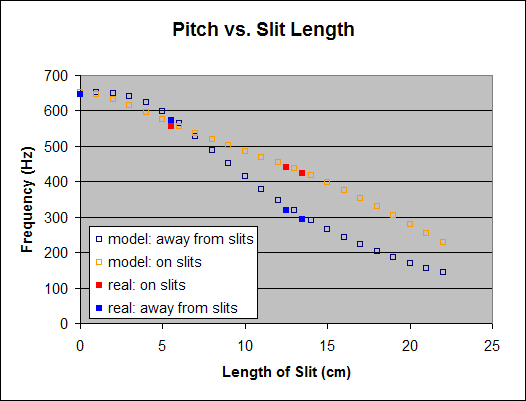
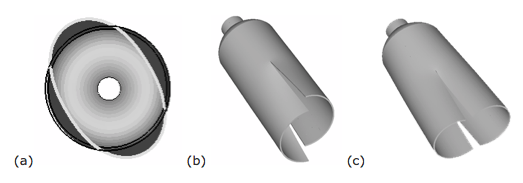
To better understand the shape of this graph, consider the shapes of the vibrational modes that produce these frequencies. Initially, with no slit, there are two orthongonal modes which look like the Figure 4(a). As long as the slit remains small, the modes still look essentially like this; there is one which has nodal lines along the slits at at a 90-degree angle from the slits which is slightly higher in pitch, and one which has nodal lines 45 degrees away from the slits which is slightly lower in pitch. Then, as the slit is lengthened, these two modes develop until they look more like the shear mode and “tuning fork” mode shown in Figs. 4(b) and 4(c), respectively. The longer slit gives both modes more freedom to bend and thus the wavelength of each is lengthened, lowering the frequency–but this effect is greater for the shear mode, which is why it crosses the line associated with the initially lower “tuning fork” mode.
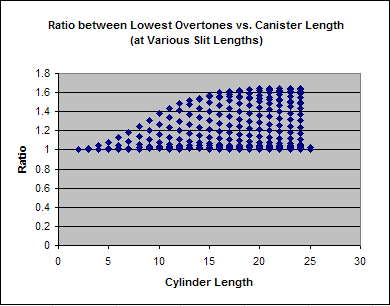
The split in the pitches of these lowest modes means that the canister sounds with a different fundamental pitch depending on where it is struck. This could be conceived as a “feature,” but it does make it difficult to play a particular tone reliably. Since the ratio between these two lowest fundamentals varies with the length of the slit, it was hoped that a canister length and slit length could be chosen that would result in a ratio of 2 to 1 (an octave).
In order to look for this ratio, additional FEA trials were run for all slit lengths of canisters between 2 and 24 cm in length. The ratio between the frequencies of the two lowest modes was then calculated for each trial and the results were plotted. Unfortunately no combinations were found in which the ratio was greater than approximately 1.64.
Conclusion
In conclusion, each of the tuning techniques investigated has a tradeoff. The method of thinning the canister is difficult from a practical manufacturing standpoint. The method of adjusting the length of the canister should result in a higher pitch, but only when the final length is fairly short. The method of adding slits to the bell seems to offer the most control, but introduces a troublesome splitting of the fundamental tone depending on where the canister is struck. It is possible that some other way of modifying the canister’s shape could be found which would allow tuning these split tones to a desirable interval, but it is not clear what shape should be tried next.








