
Time dependent probabilities and expectation values
According to the Ehrenfest Theorem, quantum mechanical expectation values coincide with classical measurements. Let's check some of these out with spin precession.Measuring $\langle S_z\rangle$
Consider the experiment of Figure 3.2:
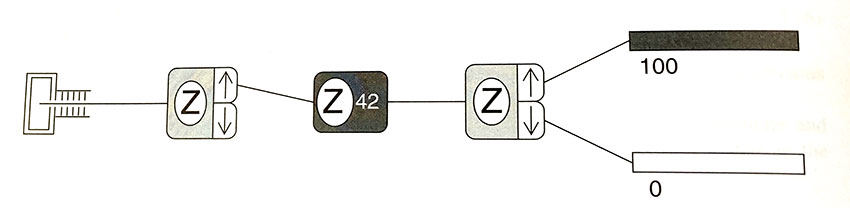
- A $\ket +$ state is prepared,
- It enters a region of magnetic field, such that at $t=0$, $\ket{\psi(0)}=\ket +$,
- It leaves the region of magnetic field at time $t$ as $\ket{\psi(t)}$ and stops changing,
- Finally it passes through a $Z$ analyzer.
The probability, $\P_+(t)$ of measuring $S_z=+\hbar/2$ for this time-varying state is given by the square of the dot product: $$\P_+ =\Big|\innerp{+}{\psi(t)} \Big|^2.$$ We have our prescription for calculating the time dependence of quantum states:
Time dependence of a quantum state
When $\hat H$ is time-independent,
- Diagonalize the Hamiltonian to find its eigenstates, $\{\ket{E_n}\}$,
- Express the initial state as a superposition of these energy eigenstates $$\ket{\psi(0)}= c_1\ket{E_1}+c_2\ket{E_2}+c_3\ket{ E_3}+...=\begincv c_1\\c_2\\c_3\\.\\.\endcv$$
- "tack on" the time-dependent term $e^{-iE_jt/\hbar}$ to each coefficient: $$\ket{\psi(t)}=\begincv c_1e^{-iE_1t/\hbar} \\c_2e^{-iE_2t/\hbar}\\c_3e^{-iE_3t/\hbar}\\.\\.\endcv$$
In this case we have $\ket{\psi(0)}=\ket +$. Since $E_+=\hbar\omega_0/2$ we find: $$\ket{\psi(t)}=\begincv 1\cdot e^{-i(\hbar\omega_0/2) t/\hbar}\\0\endcv =\begincv e^{-i\omega_0 t/2}\\0\endcv $$ So our probability is: $$\begineq \P_+ &=\Big|\innerp{+}{\psi(t)} \Big|^2\\ &=\Big|\begincv 1 & 0\endcv\begincv e^{-i\omega_0 t/2}\\0\endcv \Big|^2 =\Big|e^{-i\omega_0 t/2} \Big|^2\\ &=e^{+i\omega_0 t/2}e^{-i\omega_0 t/2}=\color{blue} 1\\ \endeq $$ Or, 100% probability of measuring $+\hbar/2$, independent of time.
In this case, the expectation value is unchanging with time, and this explains why the probability of landing in the $+\hbar$ channel in the diagram is 100%.
[A demonstration with a gyroscope wheel shows that, despite the precession of the wheel the $z$ component of spin is roughly constant in a uniform gravitational field, pointing in the $-\uv z$ direction.]
The expectation value $\langle \hat S_z \rangle$ depends on the time the system spent in the magnetic field as well, but... $$\begineq\langle \hat S_z\rangle(t) &= \bra{\psi(t)}\hat S_z\ket{\psi(t)} \\ &=\begincv e^{+i\omega_0 t/2}& 0\endcv \frac{\hbar}{2}\begincv 1&0\\0&-1\endcv \begincv e^{-i\omega_0 t/2}\\ 0\endcv \\ &={\color{blue}\hbar/2} \endeq$$ ...it's also independent of time.
Measuring $S_x$
Consider the experiment of Figure 3.4, but with a tweak:
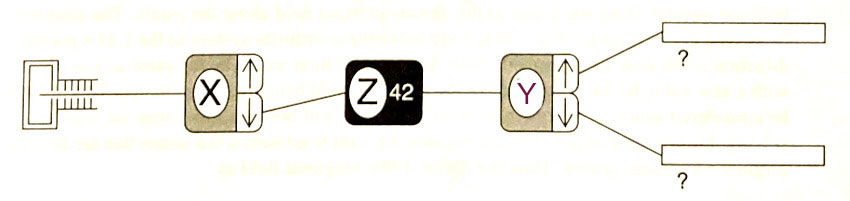
- A $\ket -_x$ state is prepared,
- It enters a region of magnetic field, such that at $t=0$, $\ket{\psi(0)}=\ket -_x$,
- It leaves the region of magnetic field at time $t$ as $\ket{\psi(t)}$ and stops changing,
- Finally it passes through a $Y$ analyzer.
The probability, $\P_{+y}(t)$ of measuring $S_{\color{purple}y}=+\hbar/2$ at the $Y$ analyzer likely depends on the time, $t$, that the particle spent in the $\uv z$-oriented magnetic field. The probability is given by the square of the dot product: $$\P_{+y} =\Big|{}_y\innerp{+}{\psi(t)} \Big|^2.$$
In this case we have $\ket{\psi(0)}=\ket -_x=\frac1{\sqrt 2}\Big(\ket + -\ket -\Big)$. Since $E_\pm=\pm\hbar\omega_0/2$ we find: $$\ket{\psi(t)}=\frac{1}{\sqrt 2}\begincv 1\cdot e^{-i\omega_0t/2}\\-1\cdot e^{+i\omega_0t/2}\endcv $$
So our probability is: $$\begineq \P_{+y}(t) &=\Big|{}_y\innerp{+}{\psi(t)} \Big|^2\\ &=\Big|\frac{1}{\sqrt 2}\begincv 1 & -i\endcv \frac 1{\sqrt 2}\begincv e^{-i\omega_0 t/2}\\ -e^{+i\omega_0 t/2} \endcv \Big|^2\\ &=\Big|\frac 12\Big(e^{-i\omega_0 t/2}+ ie^{+i\omega_0 t/2} \Big)\Big|^2 \\ &=\Big|\frac 12\Big(e^{-it'}+ ie^{+it'} \Big)\Big|^2 \\ &=... \endeq $$ To save writing, I've written this in terms of $t'$="time in units of $2/\omega_0$", that is to say: $$t'\equiv\frac{\omega_0}{2}t.$$
Continue the calculation, in whichever order is more helpful, use:
- For any complex quantity, $w$, $$|w|^2 =ww^*.$$ This is *guaranteed* to give you a real value, but you will have to work to show it!
- According to Euler's relation, $$e^{i\theta}=\cos(\theta) + i\sin(\theta)$$
- Use symmetry: $\cos(-\theta)=\cos(\theta)$ and $\sin(-\theta)=-\sin(\theta)$
...to write this result out as some real function, $A(t')$, which will be a combination of sines and cosines of $t'$.
Then without simplifying the sines and cosines (unless you see some obvious simplifictions) graph $A(t')$ in Desmos or something similar. You may have to change the variable $t'\to x$ in order to graph it.
If my guess is right, you will get a repeating function. Work out the period of that function from your graph, in terms of time $t$. E.g. when $t'=1$ then $t=2/\omega_0$; $t'=2$ corresponds to $t=4/\omega_0$, etc.
Wolfram Alpha can simplify |e^(-it)+ ie^(+it)|^2/4 to find
$$\P_{+y} = \frac12-\sin(t')\cos(t').$$
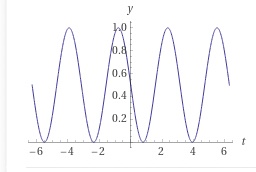
The period is $\pi$
And if you assign your complex expression a name, you can also get SageMath to do the same thing:

$\langle S_y\rangle$
We know that $\P_{-y}=1-\P_{+y}(t)=\frac12 + \frac12\sin(2t')$, so we can take a shorter approach to writing down the expectation to write down the expectation value of $S_y$: $$\begineq \bra{\psi(t)}\hat S_y\ket{\psi(t)} &= \hbar/2 \cdot \P_{+y}(t) -\hbar/2\cdot\P_{-y}(t)\\ &= \hbar/2\cdot(\frac 12-\frac 12\sin(2t')-(\frac 12 +\frac12\sin(2t')))\\ &=-\sin(2t')=\color{blue}-\sin(\omega_0t). \endeq $$
Homework 3.3
In Chapter 3, do problems 6, 12, 14, 15, and one other problem of your choosing.