Energy and time are connected

The laws of classical mechanics work just as well backwards as forwards. We say that they are symmetrical with respect to time.

Emmy Noether managed to show that conservation of energy is a consequence of the symmetry of the universe with respect to time [Classical analytical mechanics, PHYS 302]

This is the result that Zombie Marie Curie calls 'The most beautiful, deepest result in theoretical physics'.

Hamiltonian in classical physics

The Hamiltonian that we considered in 302 for a single particle, moving in 1 dimension, subject to a potential energy $U(x)$, was: $${\cal H} \equiv p\dot{x}-{\cal L}=\frac 12mv_x^2+U(x),$$ which turns out to be the total energy = kineticE + potentialE of the particle.

...and if we have such an expression for the total energy, we can calculate the time evolution, $x(t)$, for such a system.

Hamiltonian operator for our spin-1/2 particle

...in a magnetic field. We calculated this to be: $$U=- \myv{\mu}\cdot\myv{B}=-IA\uv s\cdot\myv{B} =-g\frac {q}{2m_e}\myv S\cdot\myv{B}.$$

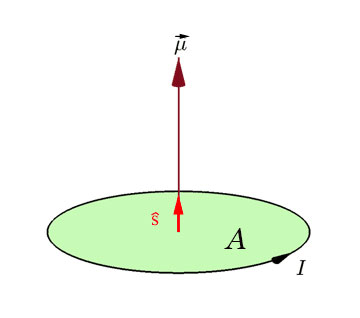Where the gyromagnetic ratio is $g\approx 2$, the charge of the electron is $q=-e$, and the spin angular momentum of the electron is $\myv S$.

Without loss of generality, let's take $\myv B=B_0\uv z$. With these relationships, the energy of a spinning electron in this magnetic field can be written in terms of a new, positive constant $\omega_0$ which turns out to have units of 1/time, as: $$E={\color{blue}\frac{eB_0}{m_e}}S_z\equiv {\color{blue}\omega_0}S_z$$

Knowing our operator $\hat S_z$, let's make the jump to define the QM Hamiltonian operator, $\hat H$, for this system as: $$\hat H=\omega_0\hat S_z \equiv \frac{\omega_0\hbar}{2}\begincv 1 & 0\\0 &-1\endcv$$

Here, the eigenstates of $\hat S_z$ are also eigenstates of $\hat H$, and satisfy an eigenvalue equation: $$\hat H\ket + = \frac{\omega_0 \hbar}2 \ket +\equiv E_+\ket +, $$ $$\hat H\ket - = -\frac{\omega_0 \hbar}2 \ket -\equiv E_-\ket -, $$ [See the energy diagram in Figure 3.1]