Operators and Matrices [2.2]

Surely you've seen these speed limit signs, which reinforce their message by showing you how fast you're going...

A wave function ket, $\ket \psi=c_1\ket{a_1}+c_2\ket{a_2}+...$ is in general a superposition of basis states, where the amplitudes $c_1$, $c_2$, ... are complex numbers.

And yet, every physical quantity we have ever measured is a real quantity.

This implies certain constraints on the operators representing physical observables:

All QM operators representing observables must be Hermitian.

Chapter highlights so far

• Diagonalizing a matrix (operator)
• Matrices that represent the operators $\uv S_z$, $\uv S_y$, $\uv S_x$, and the new one $\uv S_{\uv n}$.
• See Hermitian adjoint (p. 44)
• "In QM all operators that correspond to physical observables are Hermitian".matrices that represent "observables" (things you can measure) must be Hermitian $\Rightarrow\mym M^\dagger = \mym M$. [p. 44]
• Wave function collapse! [p. 46]

Hermitian operators

Recall from 1.2 that the Hermitian conjugate, $\mym M^\dagger$, is the complex-congugate, transpose of a matrix $\mym M$. If $\mym M$ is a square matrix, this means $$M^\dagger_{ij}=M_{ji}^*.$$

A Hermitian matrix is one which is its own Hermitian conjugate. So $$\text{Hermitian }\Rightarrow \ \ M_{ij}=M_{ji}^*.$$ This means

• $M_{ii}=M_{ii}^*$. In other words, each diagonal element of a Hermitian matrix must be real. $$\begincv {\color{#6666ff}a} & b & c\\d & {\color{#6666ff}e} & f \\ g & h & {\color{#6666ff}k}\endcv$$
• Each off-diagonal matrix element $M_{ij}$ must be the complex conjugate of its transpose $M_{ji}$ which is diagonally opposite in the matrix. $$\begincv a & {\color{#6666ff}b} & c\\{\color{#6666ff}d} & e & f \\ g & h & k\endcv$$

Hermitian matrices have two important properties:

1. The eigenvalues of a Hermitian matrix are real.
2. The $n$ eigenvectors of an $n\times n$ Hermitian matrix can always be chosen to be orthogonal, (and normalized). So they form a set of basis vectors which span the $n$-dimensional space of possible quantum states.

[Notice that the eigenvectors, $\begincv 1\\1\endcv$ and $\begincv 1\\2\endcv$ of the randomly chosen matrix of our CoCalc example Eigenvectors.pdf are *not* orthogonal.]

Confirm that the matrix representations (P. 41) of all the operators we know so far, $\hat S_x$, $\hat S_y$, $\hat S_z$, and $\hat S_{\uv n}$, are Hermitian.

In operator notation...

If a ket fulfills this eigenvalue equation, written in terms of an operator, $\hat A$ instead of a matrix: $$\hat A\ket \psi = \lambda \ket \psi,$$ then $\ket \psi$ is an eigenvector of the $\hat a$ with eigenvalue $\lambda$.

See also McIntyre's equation (2.50), in which the operator $\hat A$ is *not necessarily* a Hermitian matrix.

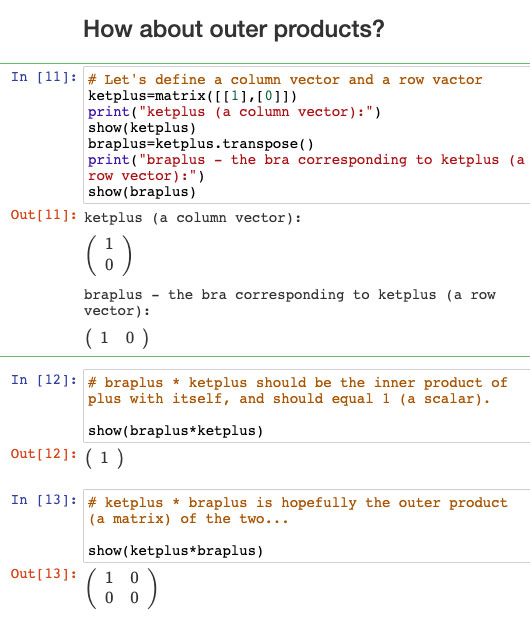
The projection operators and Outer products

The outer product of a column vector times a row vector is a matrix... $$\mym a\otimes\mym b=\mym M.$$ Top row: $a_1\mym b$, 2nd row: $a_2\mym b$, ...

In section 2.2.3, McIntyre makes plausible some projection operators, made out of outer products: "ket-bras"!

The $\hat P_+$ operator is the outer product $\ket +\bra +$. Writing this in matrix notation, and using the definitions above to write the outer product: $$\hat P_+=\ket +\bra + \equiv \begincv 1 \\ 0 \endcv\begincv 1 & 0\endcv= \begincv 1 & 0 \\ 0 & 0\endcv.$$

Calculating outer product in CoCalc works pretty intuitively... welllll intuitively, as long as you remember to define and order your row and column vectors appropriately!

Why is this called a projection operator? Consider what happens when $\hat P_+$ operates on the state $\ket \psi=a\ket + + b\ket -\equiv \begincv a\\b \endcv$: $$\hat P_+\ket \psi = \begincv 1 & 0 \\ 0 & 0\endcv\begincv a\\b \endcv = \begincv a\\0 \endcv=a\begincv 1\\0 \endcv=a\ket +.\label{Pplus}$$

Generally, the operator formed by adding together all the basis ket-bra's: $$\sum_{i=1}^n \ket{a_i}\bra{a_i} = \mathbb 1$$.

Wave function collapse!

For the ket $\ket\psi = a\ket + +b\ket -$, the probability that a $Z$ analyzer will measure $S_z=+\hbar/2$ is $$\P_+=|\innerp +\psi |^2=|a|^2.$$ But this can also be written in terms of the $\hat P_+=\ket +\bra +$ operator as (2.61): $$\begineq \P_+ &=|\innerp +\psi |^2\\ &=\big(\innerp +\psi \big)^*\innerp +\psi=\innerp \psi+\innerp +\psi\\ &=\bra\psi\hat P_+\ket \psi. \endeq$$

Let's revisit the transforming effect of the $\hat P_+$ operator, eq ($\ref{Pplus}$), $\hat P_+\ket \psi =a\ket +$... When $\hat P_+$ operates on some general state $\ket \psi$, we're left with the particle in the $\ket +$ state, multiplied by the amplitude $a$.

$\ket +$ is the state that emerges out of the spin-up channel of a $Z$ analyzer. It turns out that we can describe the output state of the spin up channel using details about the measurement by a $Z$ analyzer performed on some particular input state $\ket \psi$: $$\begineq \ket + &= \frac{a\ket +}{a}\\ &=\frac{\hat P_+\ket\psi}{\sqrt{|a|^2}} = \frac{\hat P_+\ket\psi}{\sqrt{|\innerp{+}{\psi}|^2}}= \frac{\hat P_+\ket\psi}{\sqrt{\P_+}}\\ &=\frac{\hat P_+\ket\psi}{\sqrt{\bra\psi \hat P_+ \ket\psi}}\\ \endeq $$

Amazing! Using just a projection operator and the input state $\ket \psi$ to a $Z$ analyzer, we can describe all these aspects of the measurement process of a $Z$ analyzer:

• Measurement transforms an initial $\ket \psi \to \ket{\psi'}$, into a possibly different final state. If $\ket{\psi'}\neq \ket{\psi}$, then the process of measurement is irreversible (unlike classical physics). The state $\ket \psi$ "collapses" into $\ket \psi'$.
• With probability $\P_+ =\bra{\psi}\hat P_+\ket\psi$, the analyzer measures $S_z=+\hbar/2$ and the final state will be $$\ket {\psi'}=\ket + = \frac{\hat P_+\ket\psi}{\sqrt{\bra\psi \hat P_+ \ket\psi}}$$
• [Similar things are known, using $\hat P_-\ket \psi$.]

Postulate 5 (p 46) generalizes these observations to measuring apparatuses that have any number of eigenstates.

The output states of a measuring apparatus are limited to the eigenvectors of the measuring apparatus that you've chosen.