Enthalpy and phase transitions

Enthalpy and heat of formation
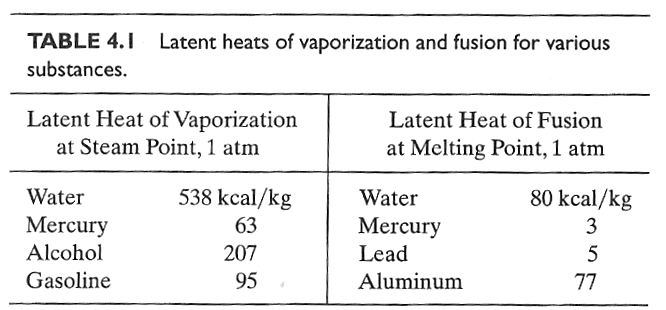
 As
a substance goes through a phase transition it absorbs (or gives off) heat even though its temperature does not change. This goes by names like "heat of formation", or "latent
heat".
As
a substance goes through a phase transition it absorbs (or gives off) heat even though its temperature does not change. This goes by names like "heat of formation", or "latent
heat".
Phase transitions are processes that:
- are isothermic
- are isobaric (constant pressure)
- involve a volume change $\rightarrow$ work is done.
How much work? $$\Delta w = P(v_2-v_1).$$
The 1st Law says... $$du = \delta q -P\,dv.$$
So, the heat change (latent heat$\equiv l$) for a macroscopic change in phase is: $$(u_2-u_1) = l - P(v_2 - v_1).$$
Solving for $l$: $$l = (u_2+Pv_2) - (u_1+Pv_1).$$
Let's define the combination in parenthesis as the specific enthalpy:
$$h \equiv u+Pv.$$
So we say that the latent heat associated with the phase transition is just
the difference in enthalpies between the phases.
$$l = h_2-h_1.$$
Enthalpy: Energy needed to create something out of nothing
...while out in the open on Earth
Most things that happen "out in the open" on Earth's surface are happening under constant pressure conditions. On Earth, atmospheric pressure is usually close to 1 atmosphere $\approx 10^5$ Pa.
Daniel Schroeder ( in An Introduction to Thermal Physics) points out...

Some folks who you might not recognize as magicians, are routinely::
- converting reactants to products with chemical reactions. These chemists just love to have tables of enthalpies of their reactants and products at "STP" because the difference is just the total energy required (or released) for reactions in open containers.
- converting humid, hot air into dry, cool air. These HVAC technicians just love having tables of enthalpies of air at different temperatures and humidities (but 1 atm of pressure) because the difference is just the total energy -- including the effect of phase changes--absorbed by / supplied to a fluid (be it air / refrigerant).
Enthalpy and $c_p$
With enthalpy per kilomole, $h$, defined as: $$h \equiv u +Pv.$$
$P$, $u$, and $v$ are all state functions (have exact differentials). Therefore, enthalpy, $h$, is also a state function.
The differential form of this definition of $h$ is: $$dh = du + P\,dv + v\,dP.$$
Since $h$ is a state function, we can choose to write its Pfaffian in terms of any two thermodynamic parameters of our choosing. Choosing $h=h(T,P)$, $$dh = \left( \frac{\partial h}{\partial T} \right)_P dT + \left( \frac{\partial h}{\partial P} \right)_T dP.$$
The 1st Law says, for a reversible process, that: $$du = \delta q - \delta w= \delta q-P\,dv.$$
Substituting in the differential form of the enthalpy into this... $$\begineq \delta q&=du +P\,dv =dh -P\,dv-v\,dP+P\,dv\\ &= dh - v\,dP. \endeq$$
Subbing that Pfaffian expression for $dh$ in to this... $$\begineq \delta q&=\left( \frac{\partial h}{\partial T} \right)_P dT + \left[ \left( \frac{\partial h}{\partial P} \right)_T -v \right]_T dP. \endeq$$
So, for the particular case of constant pressure processes ($dP=0$), we have... $$\left( \delta q \right)_P = \left( \frac{\partial h}{\partial T} \right)_P dT.$$
Or... $$ \left( \frac{\partial h}{\partial T} \right)_P=\left( \frac{\delta q}{\partial T} \right)_P\equiv c_P .$$
So
$$c_p = \left( \frac{\partial h}{\partial T} \right)_P.$$
We shall see that, for an ideal gas, $$\left( \frac{\partial h}{\partial P} \right)_T = 0,$$
So that, for an ideal gas, $h(P,T) = h(T)$, and we can write the partial differential as an exact differential: $$c_p = \frac{dh}{dT} \text{ (ideal gas)}.$$
Integrating this to find the overall enthalpy: $$\int dh = h-h_0 = \int_{T_0}^{T} c_p dT \text{ (ideal gas)}.$$
Mayer's equation
A relationship for ideal gases between $c_p$ and $c_v$ can now be obtained as follows. We had two different expressions for the heat transfer $\delta q$ for reversible processes in terms of the internal energy or the enthalpy of the system. These were... $$\delta q = du + P\,dv, $$ and $$\delta q = dh -v\,dP.$$
Setting these equal, and re-arranging just a bit... $$dh - du = P\,dv + v\,dP=d(Pv).$$
Dividing by $dT$, $$\frac{dh}{dT} - \frac{du}{dT} = \frac{d(Pv)}{dT}.$$
What is $\frac{d(Pv)}{dT}$ for an ideal gas?
For an ideal gas the two first exact differentials are $c_p$ and $c_v$, and we can calculate the differential on the rate from the ideal gas law: $$\frac{d(Pv)}{dT} = \frac{d(RT)}{dT} = R.$$
Putting this all together
$$c_p - c_v = R.$$
Problem (Carter 4-6 b): Pretend Oxygen is an ideal gas with $c_v=(5/2)R$. Suppose that the temperature of 2 kilomoles of O${}_2$ is raised from 27 C to 227 C. What is the increase in enthalpy?