Energy and degrees of freedom

...In which the puzzles of the heat capacities of gases is illuminated by quantum mechanics.

Heat capacity of an ideal gas

[Keep around...$k_B=R/N_A$. But from here on out, I'll write "$k$ instead of $k_B$.]

The kinetic theory implies, with very few assumptions, $$\frac{3}{2}k_B T = \frac{1}{2}m\overline{v^2}.$$

Assuming that all of the internal energy of our ideal gas consists of its kinetic energy, we can immediately write down an equation for $U$: $$U = N\frac{1}{2}m\overline{v^2}=N\left(\frac{3}{2}kT\right) =N\left(\frac{3}{2}\frac{R}{N_A}T\right) =\frac{3}{2}nRT.$$

For a reversible process with our ideal gas at constant volume: $$\begin{align}c_v & =\left( \frac{\partial u}{\partial T} \right)_v =\left( \frac{\partial (U/n)}{\partial T} \right)_v =\left( \frac{\partial (3RT/2)}{\partial T} \right)_v \\ & = \frac{3}{2}R.\end{align}$$

Using Mayer's equation for $c_P$: $$c_P = c_v+R=\left(\frac{3}{2}+1\right)R=\frac{5}{2}R.$$

The ratio $\gamma$ is: $$\gamma= \frac{c_P}{c_v} = \frac{5}{3}=1.67.$$

This matches up amazingly well for monatomic gases:

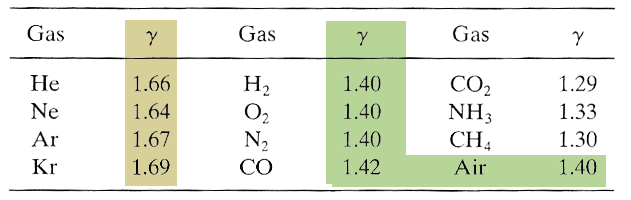
But works not as well for diatomic gases. As the number of atoms / molecule increases, $\gamma$ gets even further from 1.67.

Though, we said for diatomic gases, $C_v=\frac 52 R$, $\Rightarrow C_p=\frac 72 R$, $\Rightarrow \gamma=(7 R/2)/(5 R/2)=7/5=1.4$, so this is good.

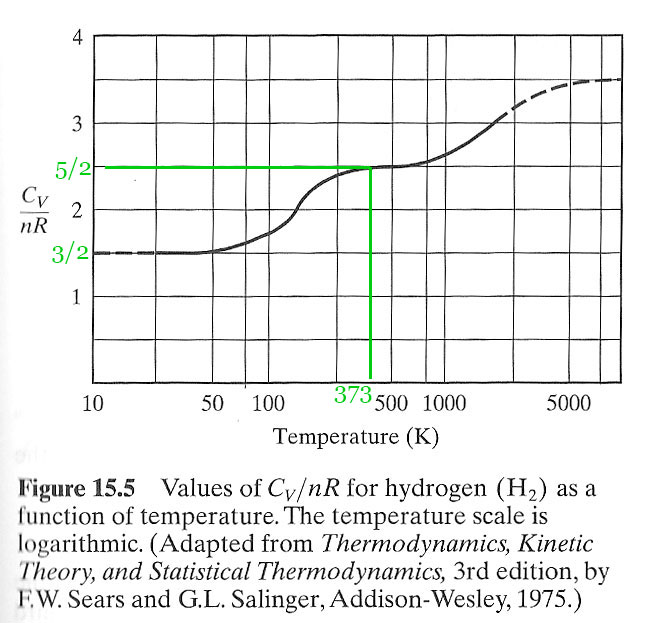
$C_v= \frac 52 R$ for hydrogen at room temperature. But, if you cool diatomic $H_2$ gas down, you find that its heat capacity $\to \frac 32R$ below about 50 K and thus $\gamma\to 5/3$ just like a monatomic gas!

Why does $C_v$ seem to follow this $(1+2n) R/2 $ pattern? And why does $H_2$ transition to $C_v=3 R / 2$ at low temperatures? (and maybe to $7 R/2$ at higher temperatures??

Degrees of freedom

The question with the Gibbs phase rule was...

How many numbers do we need to uniquely specify the [thermodynamic] state of a system?

Now, with atoms we can ask a similar question about atoms...

How many numbers do we need to uniquely specify the "state" of a single particle?

The answer is 6:

3 numbers, $x$, $y$, and $z$ to specify the position of the atom, and
3 numbers, $v_x=(dx/dt)$, $v_y$, and $v_z$ to specify the speed of the atoms.
That is, 6 degrees of freedom.

[Why don't we worry about the accelerations??]

To the extent that we have an ideal gas, with no interatom *forces*, there will be no *acceleration*. Or only accelerations during collisions of vanishingly small duration. "Most of the time" the atoms are moving ballistically between collisions...

For the simple billiard balls of an ideal monatomic gas, the energy depends only on the 3 speed numbers, not on the 3 position numbers.

We say...$\Rightarrow$ There are 3 "energy-related degrees of freedom".

If you substitute the expression $v^2=v_x^2+v_y^2+v_z^2$ into the integrals we used to find average values of things, you can readily convince yourself that $$\frac{1}{2}m\overline{v^2}= \frac{1}{2}m\left(\overline{v_x^2} +\overline{v_y^2}+\overline{v_z^2}\right).$$

Since the molecules are equally likely to be moving in any direction, the magnitudes are equal $\overline{v_x^2}=\overline{v_y^2}=\overline{v_z^2}$. This means that the energy associated with each component of velocity is the same: 1/3 for each component of the overall kinetic energy... $$\frac{1}{2}m\overline{v_x^2}=\frac{1}{3}\frac{3}{2}kT=\frac{1}{2}kT.$$

Equipartition

The equipartition theorem:
Molecules in thermal equilibrium have the same average energy associated with each independent degree of freedom of their motion: $$\frac 12 k_BT \text{ per molecule, per energy-related degree of freedom}.$$

Hyperphysics has a handy calculator, to show typical energies (~10^{-20} Joules/molecule at room temperature) and speeds (~1400 mph for a water molecule).

A molecule with more degrees of freedom has more "storage units" in which to store energy, and so, a greater heat capacity. We can calculate the internal energy of a system of $N$ molecules, each with the same $f$ degrees of freedom, as: $$U=Nf\frac{1}{2}kT =\frac{f}{2}nRT.$$

The heat capacity dependence on $f$ is... $$\begin{align}c_v & =\left( \frac{\partial u}{\partial T} \right)_v =\left( \frac{\partial (fRT/2)}{\partial T} \right)_v \\ & = \frac{f}{2}R.\end{align}$$

And $c_P$ is: $$c_P = c_v+R=\left( \frac{f}{2}+1 \right)R=\left( \frac{f+2}{2} \right) R.$$

The ratio $\gamma$ is: $$\gamma= \frac{c_P}{c_v} = \frac{f+2}{f}.$$

Diatomic gases

Counting the energy-related degrees of freedom of a two-atom gas:

linear speed: $v_x$, $v_y$, and $v_z$ specify the speed of the center of mass of the two atoms.
$\Rightarrow +3$.

spinning: If we use spherical polar coordinates $r$, $\theta$, and $\phi$ to track the position of one of the two atoms with respect to the other, then the time rates of change $\dot{\phi}$ and $\dot{\theta}$ keep track of the rotation of one atom about the other.
$\Rightarrow +2$.

harmonic oscillator (spring): The third spherical coordinate is $r$. Certainly $\dot{r}$ is related to the relative motion, and therefore the kinetic energy of the two atoms as they move relative to each other. But now, for the first time, there is also a potential energy term, which depends on the relative separation $r$ of the two atoms.
$\Rightarrow +2$.

We have $f=3+2+2=7$, so we'd expect... $$\gamma=\frac{9}{7} = 1.29.$$

The actual value (at room temperature) for the diatomic gases is closer to $1.4=7/5$ which would imply $f=5$ if equipartition is true.

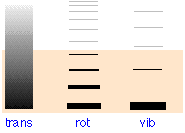The full explanation of the temperature dependence of hydrogen requires one more new thing to explain, and that is a quantum mechanics! In short:

The energy levels for translational motion in a large container are very closely spaced.
Rotational energy levels are further apart, and vibrational energy levels are even further apart.

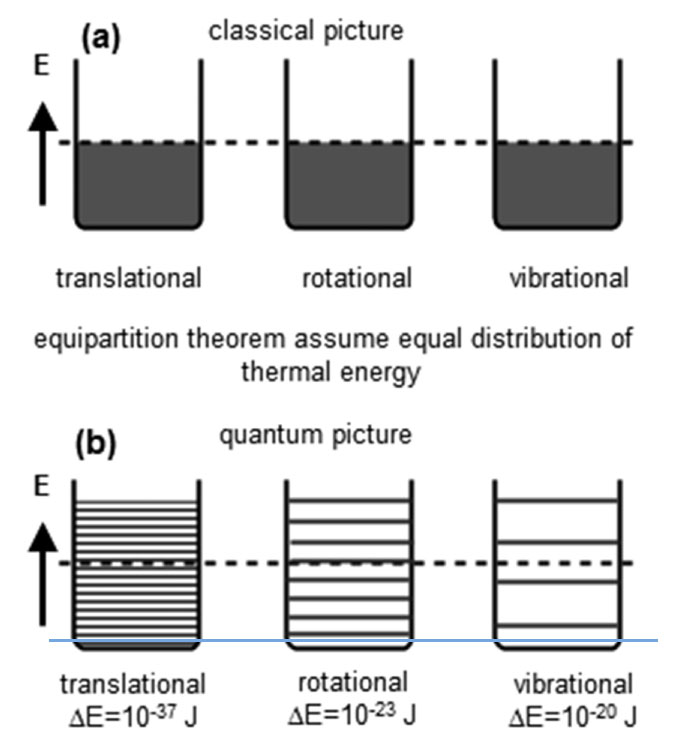
Sandeep Sharma, (2022) Kinetic Theory of Gases. In: Thermal and Statistical Physics. Springer, Cham. https://doi.org/10.1007/978-3-031-07685-5_6
At sufficiently low temperatures, none of the atoms have enough translational energy to excite another atom out of the vibrational ground state through a collision. Even more energy (~ 1000 times more) is needed to excite a molecule out of its ground state for vibrations.
See: UCDavis - ChemWiki.

Explaining the temperature dependence of the heat capacities of gases is one of the successes of quantum mechanics that Paul Dirac cited to convince folks of the necessity for and usefulness of the theory.

Are there yet more degrees of freedom that are associated with the "state" of the atom? What are their energies like compared to rotational or vibrational degrees of freedom?

I was thinking of transitions between the energy levels associated with electrons in 1s, 2p, 3d, etc orbitals. We know from the Balmer series that such a transition gives off a photon in the visible range of the E-M spectrum.

But room temperature "thermal motion" of atoms emits radiation in the far infra-red range.

The 2-d electron gas: Using Molecular Beam Epitaxy (MBE) systems you can slowly build up hybrid materials, one atomic layer at a time: You can fabricate a layered structure consisting of a very thin conducting layer sandwiched between two insulators. Electrons in the conductor form a "2 dimensional electron gas" because they can freely move within the layer, but cannot have appreciable velocities perpendicular to the conducting layer.

What should $C_v$ be for such a 'gas' of electrons?

Muddy point - Wait a second, you can excite transitions in the hydrogen atom with a laser at room temperature! (even though those transitions are spaced far apart). So why are those "degrees of freedom" not taken into account?.

That's right! But a single optical photon (from a laser) has much, much more energy than the average "thermal" energy per particle, at room temperature. What the diagram means is that there is a vanishingly small chance that a single molecule in a collection of room temperature molecules will have enough kinetic energy to excite such a transition in a collision with a hydrogen atom.

Finally, in the limit of lots of atoms per molecule, with lots of internal degrees, $f\gg 1$. If equipartition is true, $\gamma=(f-2)/f\approx 1$, when $f$ is large. So, we'd expect values for gases in the range: $$1.67 \gt \gamma \gt 1.0.$$ See this list of $\gamma$ values.

[Point out that heat capacities are not (yet) temperature dependent]