Degrees of Freedom
Mechanical systems
Our world is three-dimensional. So, will the lead car ever pass through the point $P$ shown?

The track seriously constrains where in 3-d a roller coaster car can be.
If we knew the equation for the track...What's the fewest number of variables
we'd need to uniquely specify where the tip of the lead car is?
What could that variable be?
What about...
...a skier on a mountain?

as long as she doesn't jump off the slope, can she reach any point in 3-d?
With something like a contour map in hand, or with some sort of equation that specifies all points on the surface of the mountain...What's the smallest number of variables we'd need to uniquely specify her position?
Give an example of what those variables could be.
Algebra: systems of equations
Let's say that you have three variables (unknowns) $u$, $v$, $w$.
Find values for each variable if given these 3 (constraint) equations: $$z=(y+x)^2;\ \ x-y =2;\ \ x+y=4.$$
$$\Rightarrow z=16;\ \ y=1;\ \ x=3$$ We have 0 choices about what we set the variables to. This is a point (0-dimensional object) in 3-d space.
What if I only give you 2 constraints:$$z=(y+x)^2;\ \ x+y=4?$$
$$\Rightarrow z=16;\ \ y=4-x$$
What if I only tell you: $$w=(u+v)^2?$$ [WA 'solve'...]
Thermodynamic systems
 Our prototypical thermodynamic system consists of
Our prototypical thermodynamic system consists of
- a fixed amount of one type of molecule: $n$ is a constant.
- in a piston
- in thermal contact with, say, a water bath--allowing us to control the temperature.
We can easily measure $P$, $V$, $T$. Are there 3 degrees of freedom?
In fact, if we set a particular volume (by positioning the piston) and a particular temperature, then we can't just choose any old pressure we feel like. Whenever we come back to some volume and temperature settings, $(V_1, T_1)$, then the pressure is always the same, no matter the history of how we arrived. What should we conclude?
- It would appear that we have 2 degrees of freedom.
- But since we have 3 variables, $\Rightarrow$ There must be some constraint or mathematical relationship that relates the three variables
- This constraint can sometimes be expressed as an equation, an equation of state. [What is that equation that connects $P$, $V$ and $T$ for a fixed amount of gas in our prototypical cylinder
.....
?]
Equation of state
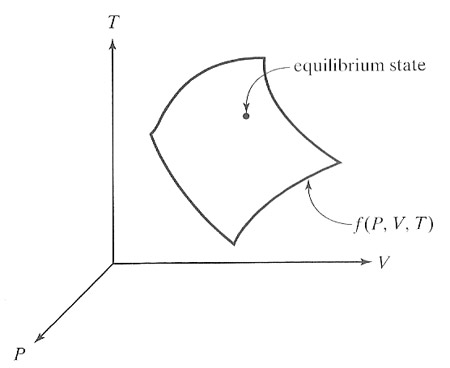 Let each thermodynamic parameter used to specify the thermodynamic state be
one dimension of a "state space". We
can plot the thermodynamic state of the system as a point in this $n$-dimensional
space.
Let each thermodynamic parameter used to specify the thermodynamic state be
one dimension of a "state space". We
can plot the thermodynamic state of the system as a point in this $n$-dimensional
space. The allowed state points are not randomly distributed in this 3 dimensional space, but are "next to" each other, so as to form a surface.
If the parameters are pressure $P$, volume $V$, and temperature $T$, then there exists a functional relationship between them written as $$f(P,V,T) = 0.$$
This reduces the number of independent variables (degrees of freedom) from 3 to 2.Ideal gas
The ideal gas 'law' is actually an empirical observation about many gases, that for nearly all of them the following relationship between pressure, volume, and temperature is approximately the same: $$PV = nRT.$$ where $n=M/m$: Mass of the system, $M$, divided by mass per molecule, $m$.
And so, we could write the equation of state as: $$f(P,V,T) = PV-nRT = 0.$$
 Kerson
Huang (in "Statistical Mechanics") writes:
Kerson
Huang (in "Statistical Mechanics") writes:"In the macroscopic domain...thermodynamics is both powerful and useful. It enables one to draw rather precise and far reaching conclusions from a few seemingly commonplace observations. This power comes from the implicit assumption that the equation of state is a regular function, for which the thermodynamic laws, which appear to be simple and naive at first sight, are in fact enormously restrictive."
Regular function
A regular function is one which in some region is:
- analytic (that is, differentiable; that is, changing "smoothly"),
- single-valued.
But which quantity in the ideal gas law is the function and which are the variables? Actually....
- $P(V,T)=nRT/V$ is a regular function of $V$ and $T$: If you know $V$ and $T$, $P$ is uniquely determined. $P(V,T)$ must pass a "vertical line" test for any values of $(V,T)$.
- $V(P,T)=nRT/P$ is a regular function of $P$ and $T$: If you know...
- $T(V,P)=PV/(nR)$ is a regular function of $V$ and $P$: If you know...
Regular functions and simple landscapes
Is the altitude (height) of Earth's surface a "regular function"?
Let the three variables be
- altitude, $h$: height above sea level,
- distance east from some reference point $x$,
- distance north from some reference point $y$.
[do $x$ and $y$ have exact or inexact differentials? That is... can they be used as coordinates?]
Is $h(x,y)$ a regular function??
Well, we have to do some averaging so as to ignore the small scale jaggedness of the landscape due to individual rocks and such...
Oh, that's just like ignoring the lumpiness of atoms when we talk about pressure, which is really some sort of averaged force (/ area) on a surface due to the impact of many atoms...
This implies that $h(x,y)$ is a regular function if we can draw a contour map of the surface.
What about this business about the height being single-valued? Which of these surfaces have a height which is always single-valued?
??

$$h(r,\theta) = 0.3*\theta??$$

(Note that $x=r\cos\theta$ and $y=r\sin\theta$).$$z(x,y)=4-x^2-2y^2$$

??

But the surface of Earth...if we don't look too closely at the details of individual rocks and such, is generally regular with just a few isolated places where it is not.
However, unlike the thermodynamic relations, $x(h,y)$ and $y(h,x)$ are not regular functions.
The missing equation of state
Most of the time we will be in the position of *not* knowing the state function, $f(P,V,T)=0$.
However, the mere assumption that there is such a surface connecting $P$, $V$, and $T$ such that each is a regular function of the others is still extremely powerful.
