Homework problems
Homework problems are from David W. Griffiths, Introduction to Electrodynamics (3rd edition).
Chapter 1:
HW #1, HW #2
Chapter 2:
HW #3,
Video Homework,
HW #4
HW #5
Chapter 3:
HW #6
Chapter 4:
HW #7
Chapter 5:
HW #8, HW #9
Chapter 12
Problems: [12.1] 3, 4, 5, 7
Notes
3
Chapter 5
HW #8
Problems: [5.1] 1, 2, 3, 4, 5, 6 [5.2] 8, 9, 10
Homework quiz Wednesday! We'll throw a dice to decide which one of these problems you'll do. (Just one part of multi-part problems).
You should memorize:
- The Lorentz force law (Eq. 5.1) $$\myv F = Q[\myv E+(\myv v \times \myv B)]$$
- The magnitude of the magnetic field a distance $s$ from an infinite wire: $$B= \frac{\mu_0I}{2\pi s},$$ and know how to use the right-hand rule to get the direction of $\myv B$.
- In cylindrical coordinates: $$d\tau = (s\,d\theta)(ds)(dz).$$
- For purposes of sanity checks, Earth's magnetic field at the surface has a magnitude of 35-70 $\mu$T. A really strong lab magnet might have a field of 1 T.
I will give you
- The B-S law for constant currents: $$\myv B(\myv r) = \frac{\mu_0}{4\pi} I\int\frac{d\myv l'\times \myv \rr}{\rr^2}$$
- The value of $\mu_0=4\pi\times10^{-7}$ N/A^2.
With distances in meters and currents in Amps, magnetic fields will have units of Teslas.
HW #9
Problems: [5.3 (mostly)] 12, 13, 14, 15, 19 [5.4] (read the notes, watch to the screencasts) 22
Notes
Problem 5.1: The charge is positive and its momentum is $p= qB\frac{(a^2+d^2)}{2d}$.
Problem 5.2
You can use the general solution (equation 5.6 in Griffiths) and fit the constants to the boundary conditions (that is, the initial velocity)
In part b, you will get expressions of the form $y(t)=\frac{E}{2B\omega}f(t)$ and $z(t)=\frac{E}{2B\omega}g(t)$.
Make a parametric plot in Desmos to see the trajectory. Let the $y$-axis represent $z(t)$
and the $x$-axis represent $y(t)$. You can plot in "units" of $E/(2\omega B)$. Here is a reminder of the syntax for parametric plotting in Desmos. (Your parameter *has* to be named $t$!)
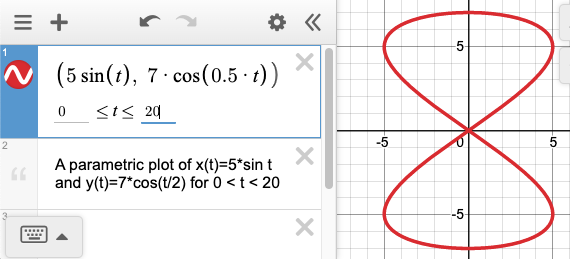
The solution in part a is no net acceleration, so particle continues in a straight line along $y$ axis.
We need to find a solution in part b with the particle starting at the origin, with $\myv v(0)=(E/2B)\uv y$.The two equations of 5.6 are... $$y(t)=C_1\cos\omega t+C_2\sin\omega t+(E/B)t+C_3.$$ $$z(t)=C_2\cos\omega t-C_1 \sin\omega t + C_4.$$ The condition that $y(0)=0$ and $z(0)=0$ implies that... $$C_1=-C_3;\ \ \ C_2= -C_4.$$ The condition that $\dot z(0)=0$ implies that $C_1=0=C_3$.
The condition that $\dot y(0)=(E/2B)$ implies that... $$(E/2B)=C_2\omega+E/B$$ That is, $C_2=-(E/2B\omega)=-C_4$.
Putting these constants into the general solution, we get $$y(t)=\frac{E}{2 B\omega}\(2\omega t-\sin\omega t\)$$ $$z(t)=\frac{E}{2 B\omega}\(1-\cos\omega t\)$$
Problem 5.5: a) $|\myv K|=\frac{I}{2\pi a}$; b) $|\myv J|(s)=\frac{I}{2\pi a s}$.
Problems: [in Chapter 3] 41 (Make sure to read the note about 41!)
4.1
Calculate the electric field between the two plates, and use that to calculate the polarization, $p$, using $E=\alpha p$ and the value of $\alpha$, given in the table for hydrogen. Then calculate the separation of charges, using $p=qd$, where $q$ is the charge (in columns) of one proton.
In the first part,
$|\myv E| = \Delta V/\text{1 mm}=500$ V $/ 10^{-3}$ m =$5\times 10^5$ V/m.
4.2
show / hide
First we need to use Gauss' Law to find the field a distance $r$ from the center. We imagine a Gaussian surface, a sphere of radius $r$, and apply Gauss' law to this sphere:
$$\begineq \oint \myv E\cdot d\myv a&=\frac{1}{\epsilon_0}Q_\text{enc}\\
E(r)4\pi r^2 &=\frac{1}{\epsilon_0}\int_{\phi'=0}^{2\pi}\int_{\theta'=0}^\pi\int_{r'=0}^r\rho(r')\,
r'^2\sin\theta'\,dr'\,d\theta'\,d\phi'\\
&=\frac{4\pi}{\epsilon_0}
\frac{q}{\pi a^3} \int_0^r e^{-2r'/a}r'^2\,dr'
\endeq
$$
Looking the integral up on WolframAlpha: 4.3
First calculate the electric field due to the cloud of charge without the nucleus. Then (superposition!) say that the total electric field that the nucleus sees is the electric field of the cloud plus the external electric field. Find the location (distance from the center) where the total electric field is zero.
show / hide
$p\propto \sqrt E$. 4.4
show / hide
$F\propto \frac 1{r^5}$.
4.5
show / hide
Torque on $\myv p_2$ is $\frac{p_1p_2}{4\pi\epsilon_0r^2}$ pointing into the page. 4.6
Assume that the dipole is free to rotate, but it's not free to move. Use the method of images with an "image dipole" on the other side of the $xy$ plane.
4.7
There are two contributions to the energy: Certainly there is the interaction energy between the two charges: Bringing one charge in from infinity costs nothing. Bring in the second charge costs $qV$, where $V$ is the potential due to the first point charge alone.
This energy will always be needed. However, if the dipole is fixed (two opposite charges, a distance $d$ apart) it will not change as we change the orientation of the dipole.
Therefore, we only need consider the energy of the two charges in the applied electric field $\myv E$. How does this depend on the orientation of the dipole with respect to $\myv E$?
4.15
I did problem 4.15 in the notes.
4.16
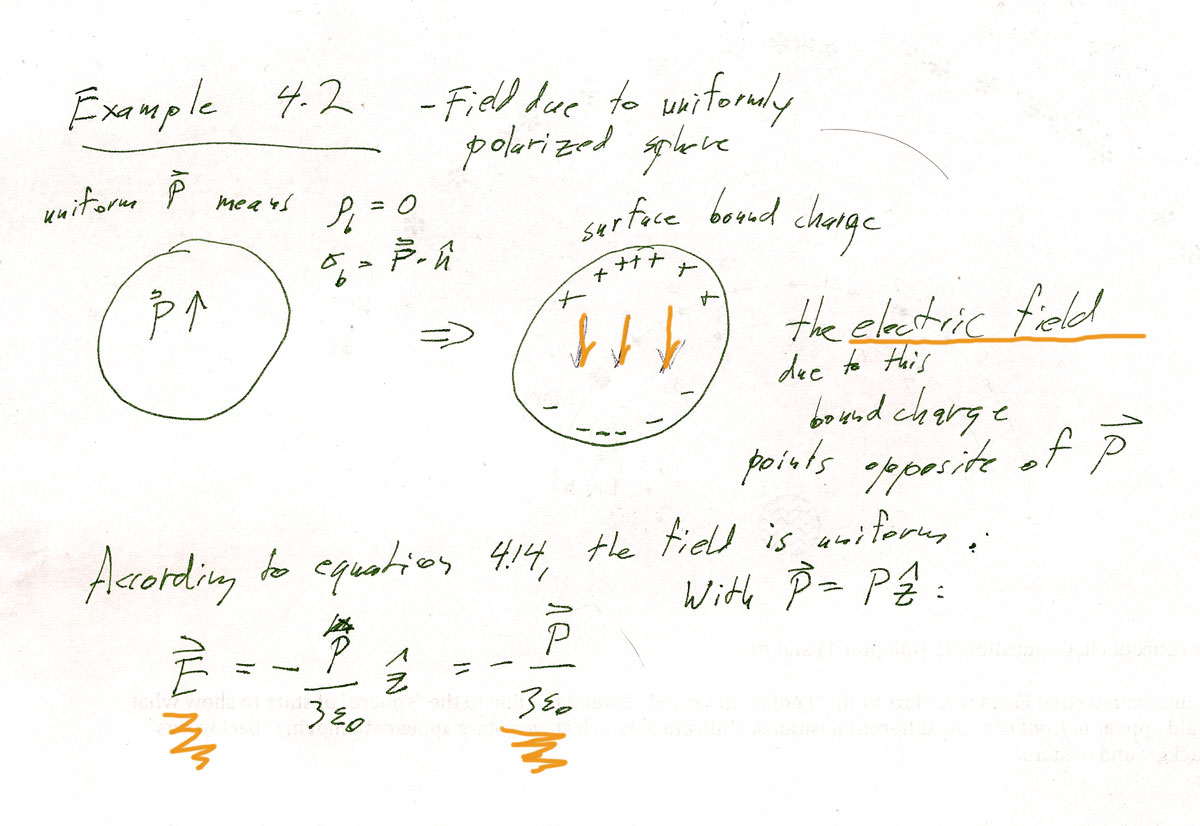
a.) In example 4.2, the electric field inside a uniformly polarized sphere was found.
Continuing to our problem: b.) According to the hint, the dielectric with the needle-shaped cavity is equivalent to a solid chunk of dielectric superimposed with a needle (long cylinder) with the opposite polarization of the dielectric in which it's embedded:
The needle with opposite polarization has a small surface density on the two small ends of $\sigma=\pm P$. But since the ends of the needle (cylinder) are far away from the center of the needle, we'll say that the electric field at the center, due to that surface charge is negligible, so the electric field at the center of the needle is $\myv E\approx\myv E_0.$ (The fields without a subscript refer to the fields at the center of the cavity.)
part c.) 4.18 The setup is illustrated in Figure 4.24: What should we assume for $\myv D$ in a conductor? Certainly we know that $\myv E=0$ in a conductor. We assumed that charge carriers are able to move completely freely in the conductor and did not invoke "polarization density" to explain the surface charge on conductors. So let's say that $\myv P=0$ in a conductor as well. Therefore
$\myv D=\epsilon_0 \myv E+\myv P = \epsilon_0 0+0=0$, so the displacement field in a conductor is also 0.
4.30 [section 3.1] 2 - see below 3.2 A particle can only be in equilibrium where $V$ has a minimum. But this is
only possible if $\grad^2V \gt 0$. Where will a positive test particle "leak" out of the box?
Assume a positive test charge $q$, and 8 equal positive charges at the vertices of a cube. Let's say at (1,1,1), (1,1,-1), (1,-1,1)... all 8 combinations of +1 and -1.
It is possible to calculate the potential along various lines through the center of the box. The electric potential is the sum of the potentials from each of the 8 point charges at the vertices of the cube.
Parameterize each of the paths below in terms of a variable, let's say $a$, and graph $V(a)$ to where it meets the boundary of the cube. We expect the forces to balance at the center. So the question is, as a function of the path parameter, is there at least one path where the potential is concave down, such that a particle at the origin could spontaneously "roll out" of the cube along that path?
Problem 41
a.) Imagine you have a point charge at position $\myv r$ in the sphere. Find an expression for the average field inside the sphere...
This problem requires that you think rather carefully about how you
label positions. Generally, we use $\myv \rr=\myv r-\myv r'$ to indicate
the separation vector between say, $\myv r'\equiv$the position of some charge, and $\myv r \equiv$the location
where you wish to evaluate the field. In this problem, we're going to use those positions differently:
Continue on to write out the expression for the average which includes an integral
which you do not need to evaluate!
The sphere with a radius $R$ has a volume, ${\cal V} = \frac{4}{3}\pi R^3$.
So, the average of the electric field over the volume ${\cal V}$ is
$$\myv E_\text{ave}(\myv r) = 1/ {\cal V} \int_{\cal V} \frac{1}{4\pi \epsilon_0} \frac{q*(\myv r' - \myv r)}{|\myv r'-\myv r|^3} d \tau'.$$
You don't actually have to solve the integral.
But in the next part of part a) your goal is to show that with the uniform charge density given, you get exactly the same expression. Make sure that you explicitly say what the meaning is of each of the two vectors $\myv r$ and $\myv r'$ in this second part of the problem.
[section 2.1] Choose either problem 2.15 or 2.17 to make a video presentation of the problem.
For either one, you'll need to sketch the setup. You may scan-and-adapt the diagrams in the book.
[Originally, I said "Make a careful symmetry argument. Explain your volume and surface integrals." Expanding on this...]
Some things to be sure and include:
Look for symmetry: Ways in which the charge in one part of the system is exactly balanced by charge elsewhere in the system. Are there some rotational or mirror symmetries? E.g. can you say "the field here is the same as over there, because...." or "the field here is exactly opposite the field over there, because...".
For problem 17 it is very useful to be able to show that $\myv E$ is only ever parallel to $\hat y$ and that $\myv E(y)= -\myv E(-y)$.
[2.3] 20, 21, 22, 26, 28 [2.4] 31, 32, 33, 34, 46
2.1
Hint for part d) - Use the principle of superposition: Once you've decided on an answer for part c): What charge (and where) could you *add* to the set of charges in part c) to get the desired total charge distribution of part d)?
c) Talking about this in class, Paul showed that the forces balance for 3 charges arranged in a circle around a point. We made a grounded *guess* that symmetry sez net force = 0 in this case too. 2.2
We did the first part of problem 2.2 in class, though the answer is not recorded in the notes.
part b: also find the far-field limit for $z\gg d$. We shall that this is the field of a dipole.
In the far field limit $z\gg d$, this becomes:
$$\myv E(0,0,z)\uv x\approx\frac 1{4\pi\epsilon_0}\frac {qd}{z^3}\uv x.$$
We will see that a dipole consists of two opposite charges, $q$ and $-q$ separated by a distance $d$. Defining the dipole as a vector $\myv p$ where $|\myv p|=qd$ directed from the positive to the negative charge, this is the field along $z$ of an ideal dipole at the origin, directed in the $+\uv x$ direction.
$$\myv E(0,0,z)=\frac 1{4\pi\epsilon_0}\frac {\myv p}{z^3}.$$
2.3
Do two different integrals: one for the $x$ component of the field, one for the $z$ component of the field. [Example 2.2 may be helpful.]
Everybody got the exact answer (yay!) But how do you take the
$z\gg L$ limit? And what should you expect for the electric field in this limit??
Some of you wrote "$L\approx 0$". But if this were true you'd have $\myv E \to 0$, and none of you wrote 0 as the limit.
Instead, think more narrowly about terms that involve sums of $z$ and $L$ terms.
We *can* say that when $z\gg L$ then $z^2+L^2\to z^2$, and then
$\sqrt{z^2+L^2}\to\sqrt{z^2}=z$. With this replacement, our electric field approaches
$$
\begineq\myv E(0,0,z)&=
\frac{1}{4\pi\epsilon_0}\frac{\lambda}{z}\left[
\left( -1+\frac{z}{z}\right)\uv x+
\left( \frac{L}{z}\right)\uv z
\right]\\
&=
\frac{1}{4\pi\epsilon_0}\left[
\frac{\lambda L}{z^2}\,\uv z
\right]\endeq
$$
Oh, this looks like the field along the $z$ axis of a single point charge at the origin, where the point charge is $Q=\lambda L$. And if you think about the units, indeed, $L\lambda$ is the total charge of a line charge of length $L$ meters with a linear charge per meter of $\lambda$.
2.5
The answer is in the notes, but you should show how you set up the integral, and then solve it.
2.6
One goal of this problem is to get you up to speed once more for using CoCalc. The answer is in the notes, and the start of the integral.
You should show how you set up the integral in your problem write up. Then use CoCalc (a notebook in your /HW/HW #3 folder ). In your notebook use a markdown cell to display the integral you're going to solve, then use Sagemath to do the integration (and perhaps simplify the result).
2.10
Use the divergence theorem to relate electric field flux to enclosed charge. You won't need to actually carry out any integral to calculate the answer.
Hint: Think about placing the charge at the very center of a larger cube, made up of 8 cubes with identical dimensions to the one pictured in figure 2.17.
Now imagine that the 8 cubes all share a vertex at the location of the charge. This larger cube completely encloses the charge, so you can (easily?!) evaluate the total flux through the outside surfaces of the larger cube. Calculate that total flux. (Again, you won't need to actually carry out any integral.) I think at that point you will see what to do next to answer the original question...
2.13
$\myv E(s,\phi, z)=E_s(s)\uv s$ where
$$E_s(s)=\lambda/(2\pi\epsilon_0 s).$$
2.17
Make an argument that $\myv E$ will only have a $y$ component, and then design your Gaussian box to have surfaces that are either perpendicular or parallel to $\uv y$. Can symmetry alone tell you the magnitude of the electric field anywhere?
At some point, you need to have a box with a finite area, $A$, perpendicular to $\uv y$. But hopefully $A$ will drop out of your final expressions for the field, since the enclosed charge will also be proportional to $A$.
2.18
Using the principle of superposition... View this problem as the sum of two symmetric charge distributions, for which you can calculate the electric field using Gauss' law; For which we *did* calculate the electric field (see 2.12). You should find that the electric field inside *one* of the spheres is proportional to $\myv r$: the position vector of the location at which we want $\myv E(\myv r)$. Call $\myv r_+$ the location relative to the center of the sphere that has a positive charge distribution, and $\myv r_-$ the location relative to the center of the sphere that has a negative charge distribution. You'll need to draw a vector diagram to calculate the electric field, and that should be enlightening...
2.20
In the last part, to find the potential, you need to integrate from a starting point to the final point $\myv r=\myc{x,y,z}$. You can integrate from any convenient reference point to the final point. You should find,
$$V(x,y,z)=-\int \myv E\cdot d\myv l=-k(xy^2+yz^2) +C$$
where the constant depends on the "starting point" of your line integral.
Using the paths shown, we have:
$$V(x,y,z)=-\int_I\myv E(x',y',z')\cdot d\myv l' -\int_{II}\myv E\cdot d\myv l'
-\int_{III}\myv E\cdot d\myv l'$$
where we're using the curl-less field from part b: $\myv E(\myv r)=k\myc{y^2,(2xy+z^2),2yz}$.
2.22
Instead of setting $V(s)\left.\right|^{s=\infty}=0$, this time set our zero point to $V(s)\left.\right|^{s=a}=0$. Once you solve the problem using $s=a$ as the zero point, see what the consequences would have been of setting $V(s)\left.\right|^{s=\infty}=0$.
Using Gauss' Law you can figure out that (Problem 2.13) $\myv E(s,z,\theta)=
\frac{1}{4\pi\epsilon_0}\frac{2\lambda}{s}\uv s$. Setting $V=0$ at $s=a$, we get
$$V(s)=-\int_{s'=a}^s\frac{\lambda}{2\pi\epsilon_0}\frac1{s'}ds' = \frac{\lambda}{2\pi\epsilon_0}\ln\left(\frac sa\right).$$
*Why* can't we do the usual thing of $V(\infty)=0$?
As you can readily see, setting $a=\infty$ or $a=0$ give unusable potentials, but in this form, if you take $-\myv\grad V=\myv E$ of this $V$ to get the electric field, you will recover the electric field that we started with.
2.26 - Integrate over all the charge directly, using as integration variable the distance $\rr$ from the vertex to a point on the surface of the cone,
surface of the cone -OR- $z$, the vertical distance above the vertex. 2 ways to set up the integral (Part a of 2.26), narrated, 9 min
To find the potential at point b, your integration variable will be $h$ or a new variable (call it something other than $\rr$ !) that could be the distance from $\myv a$ along the cones surface. But this time you'll have a more complicated expression for the distance from $\myv b$ to a point on one of those "circles of charge". The answer is $$V(b)=\frac{\sigma h}{2\epsilon_0}\ln(1+\sqrt 2).$$
Show your work, and show clearly the (complicated) integral you had to solve, and the solution for the integral you found (via WolframAlpha or CoCalc).
$$V(b)=\frac{1}{4\pi \epsilon_0}\int \frac{dq}{\rr'}
=\frac{1}{4\pi \epsilon_0}\int_0^{\sqrt 2 h}\frac{2\pi\rr\sigma}{\sqrt 2 \rr' }d\rr,
$$
Therefore the potential difference is
$$V(a)-V(b)=\frac{\sigma h}{2\epsilon_0}\[1-\ln(1+\sqrt 2)\].$$
2.28 At this point, it's necessary to distinguish between two cases, $r \gt z$
and $z \gt r$.
For $r \gt z$, $$\int = \frac{4}{(r-z)+(r+z)}=\frac{2}{r}$$
for $r \lt z$, $$\int = \frac{4}{(z-r)+(r+z)}=\frac{2}{z}$$
2.35 2.38 integrating the $z$ component of the force over the top half of a sphere should give the total force on the top hemisphere.
There is a charge $Q$ on a conducting sphere of radius $R$. Since there is not other charge or field around, the charge must be spread out uniformly over the surface of the sphere (total surface area $4\pi R^2$, so
$$\sigma=\frac{Q}{4\pi R^2}.$$
According to Griffiths' Eq (2.51), the force per unit area for surface charge on a conductor is:
$$\frac{\myv F}{A}=\myv f=\frac{1}{2\epsilon_0}\sigma^2\uv n$$
Using the surface charge density calculated, and recognizing that the surface normal for a sphere is $\uv r$, this can be written as
$$\myv f=\frac{1}{2\epsilon_0}\left( \frac{Q}{4\pi R^2} \right)^2\uv r
=\frac{Q^2}{32\epsilon_0\pi^2R^4}\uv r.$$
Now imagine the sphere is centered at the origin. The total force in the $\uv z$ direction on the upper half should be equal and opposite to the total force integrated over the lower half. So, let's integrate the component of the force in the $\uv z$ direction. That is, integrate $(d\myv F)_z=(df\,da)\cos\theta$, where $da=R^2\sin\theta\,d\theta\,d\phi$ is the size of a patch of surface aread on the sphere. Thus:
$$\begineq(\myv F)_z&=\int_{\phi=0}^{2\pi}\int_{\theta=0}^{\pi/2} \frac{Q^2}{32\epsilon_0\pi^2R^4}R^2\sin\theta\,\cos\theta\,d\theta\\
&=\frac{Q^2}{32\epsilon_0\pi^2R^2}
2\pi\int_{\theta=0}^{\pi/2}
\sin\theta\,\cos\theta\,d\theta\,d\phi\\
&=\frac{Q^2}{32\epsilon_0\pi^2R^2}
2\pi\left(\frac 12\right)
=\frac{Q^2}{32\epsilon_0\pi R^2}
\endeq$$
Where I've used WolframAlpha to do the $\theta$ integral. 2.39
Apply Gauss' Law to find the electric field:
$$\oint \myv E\cdot d\myv a = Q_\text{enc}/\epsilon_0$$
using a Gaussian surface, consisting of a cylinder of radius $s$ and length $L$.
2.48 [section 1.1] 2, 3, 4, 5, 7, 10abc
[1.3] 29, 31, 32, 33,
1.2
Can you think of a counterexample using the unit vectors $\uv x$, $\uv y$, and $\uv z$? (Use the right hand rule to work out individual cross products of these...)
1.3 -- You can use the same approach as example 1.2.
Doing the calculations in SageMath: 1.4
The cross product of any two vectors (in the plane) will be perpendicular to the vectors (and thus perpendicular to the plane). Connect points in the plane (using Figure 1.11) to come up with some vectors in the plane.
Doing the calculations in SageMath: 1.10(a)
Beware: The original vector $\myv r$ in Eq. (1.19) goes from the original origin to the original point $P$. When you translate the coordinate system, there is a new origin, $\bar{\cal O}$, and the point, $\bar P$, has new coordinates. But the vector $\myv r$ still goes from the original origin to the original point $P$.
If a vector $\myv v$ runs from (tail) $(0,0,0)$ to (head) $(l,m,n)$ then its components are $\langle l,m,n\rangle$. Say that the vector $\myv V$ has components $\{l,m,n\}$ in the original coordinate system. Give its components $\{l',m',n'\}$ in the new coordinate system in terms of $l$, $m$, and $n$. (And for some of these problems, you may also need to calculate coordinates in the new coordinate system for the original origin.)
1.10(b)
If a vector has components $\myv v=\langle l, m, n\rangle$, then in the inverted coordinate system the vector will have components $\langle -l,-m,-n \rangle$. A regular vector is transformed under coordinate inversion as $\myv v \to -\myv v$.
1.10(c)
You might want to do this one with a particular set of vectors $\myv A \times \myv B = \myv V=\{l,m,n\}$.
In the inverted system, find the components of $\myv A'$ and $\myv B'$, and then find their cross product, $\myv V'$, using equation 1.14. Now see how the components of $\myv V'$ relate to $\myv V$.
Two vectors $\myv A$ and $\myv B$ will be transformed by coordinate inversion into $-\myv A$ and $-\myv B$.
1.11
a) $\myv \grad f=2x\uv x+3y^2\uv y+4z^3\uv z$
1.12 - What does the answer mean in terms of miles north/south and miles east/west of South Hadley?
a.)You were asked about the peak position relative to
South Hadley.
The answer, peak at (-2,3), means 2 miles west (negative east) and 3
miles north of South Hadley.
1.13
Use the Cartesian representation of the separation vector (See equations 1.26-1.28).
The gradient operator $\myv \grad$ in this problem is
$$\myv \grad=\uv x\frac{\del}{\del x} +\uv y\frac{\del}{\del y} +\uv z\frac{\del}{\del z}$$
and only operates on $x$, $y$, $z$. That is, treat $x'$, $y'$, and $z'$ as constants.
FYI, later on (not in this problem!) you will be taking derivatives with respect to the primed variables instead, using this operator:
$$\myv \grad'=\uv x\frac{\del}{\del x'} +\uv y\frac{\del}{\del y'} +\uv z\frac{\del}{\del z'}$$
$\myv \rr=(x-x')\uv x+(y-y')\uv y+(z-z')\uv z$, and therefore the magnitude of this vector is $\rr=\left[(x-x')^2+(y-y')^2+(z-z')^2\right]^{1/2}$.
1.15
a) $\myv \grad \cdot \myv v_a=2x + 0 -2x=0$
1.25
c) The answer is zero!
a) $\grad^2T_a=2$
1.27 - The proof involves writing out the components of the cross product of the gradient of a scalar function $\color{purple}f(x,y,z)$. Look back to Calc III to recall what we know about the order of differentiation of a smoothly varying function: Clairaut's Theorem.
1.29
1.30
When you're asked: "Does the surface integral depend only on the boundary line for this function?"... You would need to make a calculation of a different surface that shares the same boundary line and see if they agree or not. Example 1.7 calculates the flux over a 5-sided surface that does indeed share the same boundary line. So, compare your answer to the sum of the integrals in example 1.7.
In the first part "upward" is the positive direction, so $$d\myv a = dx\,dy\,\uv z$$
You have to solve the double integral...
$$\begineq \int_0^2\int_0^2 \myv v(x,y,z=0) \cdot dx\,dy\,\uv z\endeq$$
$$\begineq \int_0^2\int_0^2 \myv v(x,y,z=0) \cdot dx\,dy\,\uv z
&=\int_0^2\int_0^2 v_z(x,y,z=0) \, dx\,dy\\
&=\int_0^2\int_0^2 -3y dx\,dy\ \\
&=\int_0^2 -3y\,dy \left(\int_0^2 dx \right)\\
&=\int_0^2 -6y\,dy=-12.
\endeq$$
The four edges around the "bottom of the
box" in Fig. 1.23 form the boundary line of both:
The flux "up" through the top five squares (Example 1.7) was 20.
You should have just figured that the flux "up" through the bottom surface was -12: Not the same as out through the 5 other surfaces. So apparently the surface integrals of this function do not depend exclusively on the boundary line.
[Really, these flux integrals would only be guaranteed to be the same if the vector field $\myv v$ is the curl of some other vector function (called a "vector potential"), that is, if $\myv v= \myv \grad \times \myv A$. So, we could conclude that there's *no way* that we could write $\myv v = 2xz \uv x+(x+2)\uv y +y(z^2-3)\uv z$ as the curl of some vector potential $\myv A$.]
As for the total flux out of the box, we need to add the flux out through the surfaces of Ex 1.7., (20) to the flux outward through the bottom surface of the box.
To find the outward flux, we do the same integral as in the first part, but this time the surface normal is $d \myv a=-dx\,dy\,\uv z$, so it's just (-1) times the previous answer, or +12.
1.31 - Here is a review of line-integral strategies to find "Work"-like quantities along a particular path.
We want to verify the fundamental theorem for gradients--Equation (1.55)--which claims that the line integral of the tangential component of (the gradient of a scalar function ) along a particular path depends only on the starting and ending points, and not on the details of a particular path:
$$\int_{\myv a}^{\myv b}\left(\myv \grad T\right)\cdot d\myv l
=T(\myv b)-T(\myv a).$$
The function we're interested in is $T(x,y,z)=x^2+4xy+2yz^3$. As you should verify, its gradient is
$$\myv \grad T=(2x+4y)\uv x+(4x+2z^3)\uv y+(6yz^2)\uv z.$$
And, the value that we expect for each integral should be 7, because:
$$\begineq T(1,1,1)-T(0,0,0)&=(1^2+4*1*1+2*1*1^3)-0\\
&=1+4+2=7.\endeq$$
a.) The differential in the integral can be written most generally as
$d\myv l = dx\,\uv x+dy\,\uv y+dz\,\uv z$.
Along the first line segment from $(0,0,0)$ to $(1,0,0)$ we have $d\myv l=dx\,\uv x$, and $y=0;\ z=0$. So
$$\begineq
\int\left(\myv \grad T\right)\cdot d\myv l
&=\int_{x=0}^{1}\left(\myv \grad T\right)_x\,dx\\
&=\int_{x=0}^{1}\left.\left( 2x+4y\right)\right|^{y=0;z=0}\,dx\\
&=\int_{x=0}^{1}\left( 2x\right)\,dx=\left.x^2\right|_{x=0}^{1}=1\\
\endeq
$$
Continue by finding the integrals along the 2nd and 3rd segments, and add the results together.
b) Along the 2nd line segment from $(1,0,0)$ to $(1,1,0)$ we have $d\myv l=dy\,\uv y$, and $x=1;\ z=0$. So
$$\begineq
\int\left(\myv \grad T\right)\cdot d\myv l
&=\int_{y=0}^{1}\left(\myv \grad T\right)_y\,dy\\
&=\int_{y=0}^{1}\left.\left( 4x+2z^3\right)\right|^{x=1;z=0}\,dy\\
&=\int_{y=0}^{1}\left( 4\cdot 1 \right)\,dy=\left.4y\right|_{y=0}^{1}=4\\
\endeq
$$
b.) For this path, the first line segment runs from $(0,0,0)$ to $(0,0,1)$ and we have $d\myv l=dz\,\uv z$, and $x=0; y=0$. So
$$\begineq
\int\left(\myv \grad T\right)\cdot d\myv l
&=\int_{z=0}^{1}\left(\myv \grad T\right)_z\,dz\\
&=\int_{z=0}^{1}\left.\left( 6yz^2 \right)\right|^{x=0;y=0}\,dz\\
&=\int_{z=0}^{1}(6\cdot0\cdot z^2)\,dz=0
\endeq
$$
Continue by finding the integrals along the 2nd and 3rd segments, and add the results together.
Along the 2nd line segment from $(0,0,1)$ to $(0,1,1)$ we have $d\myv l=dy\,\uv y$, and $x=0;\ z=1$. So
$$\begineq
\int\left(\myv \grad T\right)\cdot d\myv l
&=\int_{y=0}^{1}\left(\myv \grad T\right)_y\,dy\\
&=\int_{y=0}^{1}\left.\left( 4x+2z^3\right)\right|^{x=0;z=1}\,dy\\
&=\int_{y=0}^{1}\left( 2\cdot 1^3 \right)\,dy=\left.2 y\right|_{y=0}^{1}=2\\
\endeq
$$
c.)
Another way to set up a path integral is to parameterize the path of integration. That is, we describe the path in terms of the three functions $x(t)$, $y(t)$ and $z(t)$ where $t$ is a scalar running from some initial $t_i$ to a final value of $t_f$. Then the path integral can be written as:
$$\int_{\myv a}^{\myv b}\left(\myv \grad T\right)\cdot d\myv l=
\int_{t_i}^{t_f}\left(\myv \grad T(x(t),y(t),z(t)\right)\cdot \frac{d\myv l}{dt}\,dt,$$
where $\frac{d\myv l}{dt}=\langle\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\rangle$.
$$\begineq \int \left(\myv \grad T\right)\cdot d\myv l
&= \int_{x=0}^{x=1}
\left.\myc{2x+4y,4x +2z^3,6yz^2}\right|^{x=x; y=x; z=x^2}\cdot\myc{1,1,2x}\,dx\\
&= \int_{x=0}^{x=1}
\myc{2x+4x,4x +2(x^2)^3,6(x)(x^2)^2}\cdot\myc{1,1,2x}\,dx\\
&= \int_{x=0}^{x=1}
\left(6x\ \ +4x +2x^6)\ \ +6x^5*2x\right)\,dx\\
&= \int_{x=0}^{x=1}
\left(10x +14x^6\right)\,dx = \left.(5x^2+2x^7)\right|_{x=0}^{1}=5+2\\
&=7
\endeq
$$
1.33
Stokes' theorem claims that
$$\int_{\cal S}\myv \grad \times \myv v\ \cdot d\myv a
=
\oint_{\cal P}\myv v \cdot d\myv l
.$$
We'll be testing $\myv v=\myc{xy,2yz,3zx}$
and its curl is (CoCalc or Mathematica):
$$\myv \grad \times \myv v=\myc{-2y,-3z,-x}.$$
For the surface integral, you'll have $d\myv a=dy\,dz\,\uv x$.
The surface integral becomes...
$$\begineq \int_{\cal S}\myv \grad \times \myv v\ \cdot d\myv a &=
\iint \myv\grad \times \myv v \cdot \uv x\,dy\,dz\\
&=\int_{y=0}^2\int_{z=0}^{2-y} (\myv\grad \times \myv v)_x\,dz\,dy\\
\endeq$$
[Work this from here on. The answer is $-8/3$.]
$$
\begineq \int_{\cal S}\myv \grad \times \myv v\ \cdot d\myv a
&=\int_{y=0}^2\int_{z=0}^{2-y}[ (-2y)\,dz]\,dy\\
&=\int_{y=0}^2(-2y) (2-y)\,dy=\int_{y=0}^2(2y^2-4y)\,dy=-\frac 83.
\endeq$$
$$ \myv v = xy \uv x+2yz\uv y+3zx\uv z$$
Now, compare to the line integral of $\myv v\cdot d\myv l$ around the triangular boundary. It turns out that the two straight segments give 0. :
1.37 - Work these out by trigonometry starting with Figure 1.36. Make a couple sketches to illustrate your derivations of the unit vectors.
1.38
Work these out using the spherical-polar forms for the divergence, $\myv \grad \cdot$, and the volume differential, $d\tau$.
[possible part b screencast]
a.) $\myv \grad \cdot r^2\uv r = 4r$ and both sides of the divergence theorem are $4\pi R^4$.
1.40 - Use the expressions on the inside cover to calculate the gradient and the Laplacian, in spherical coordinates. *Then* convert $T$ to Cartesian coordinates and take the gradient and Laplacian. *Then* convert yoiur spherical gradient and Laplacian to Cartesian coordinates to see if they agree.
1.60
Continuing...
$$\begineq
\int_{\cal V}\left(\frac{\del c_xT}{\del x}+\frac{\del c_yT}{\del y}+\frac{\del c_zT}{\del z}
\right)
\cdot Td\myv a
&=
\oint_{\cal S}\left(
c_x\uv x+c_y\uv y
+c_z\uv z
\right) \cdot Td\myv a\\
\\
\myv c \cdot \int_{\cal V}\left(\frac{\del T}{\del x}\uv x+\frac{\del T}{\del y}\uv y+\frac{\del T}{\del z}\uv z
\right)
\,d\tau &= \myv c \cdot \oint_{\cal S} T(x,y,z) d\myv a\\
\myv c \cdot \int_{\cal V}\myv \grad T
\,d\tau
&= \myv c \cdot \oint_{\cal S} T(x,y,z) d\myv a\\
\endeq$$
Eventually you can write both the left and the right hand sides
as $\myv c\cdot$[some integral], and the equality of the two integrals is the final result you seek.
So, the parts to the right of $\myv c\cdot$ must be equal:
. 1.61
Find the vector area $\myv a = \int_{\cal S}d\myv a$ where the surface ${\cal S}$ to integrate over is half of a sphere of radius $R$. .
You should start by making a symmetry argument that $a_x = \int da_x = 0$ and $a_y=\int da_y=0$. Support your argument with a sketch.
Then, you *only* have to worry about how to compute the $z$-component: $\left(\int d\myv a\right)_z=\int d\myv a \cdot \uv z.$ (You will find useful the relation that $\uv r\cdot\uv z = \cos\theta$.)
[Hint: I didn't ask you to do part c.). But assuming that result is true, then the answer to a.) must be a vector with the same magnitude as integrating over a *flat* surface sharing the circular boundary of radius $R$. That is, the answer must be a vector with a magnitude of $\pi R^2$.]
Putting this together:
$$d\myv a = R^2\sin\theta\,d\theta\,d\phi\,\uv r$$
Now think about the Cartesian components of $d\myv a$ with the center of the bowl, as shown, on the $z-$axis. Draw $d\myv a$ at some position $r, \theta, \phi$ on the surface of the bowl. Note that at the point at $\phi + 180^o$ on the other side of the bowl, the $x$- and $y$-components of $d\myv a$ will be exactly opposite. So, that when we integrate over the whole surface, these components will sum to zero. Ah-ha--we only need to worry about the $z$-component. That $z$-component is
$$\begineq (d\myv a)_z&=R^2\sin\theta\,d\theta\,d\phi\,\uv r\cdot \uv z\\
&=R^2\sin\theta\,d\theta\,d\phi\,\cos\theta
\endeq$$
Now we're ready to integrate that $z$-component over the surface of the bowl
$$\begineq \myv a =(\myv a)_z \uv z&= \uv z \int_0^{\pi/2} d\theta\int_0^{2\pi} d\phi
R^2\sin\theta\cos\theta
\\
&= \uv z R^2 2\pi \int_0^{\pi/2} d\theta
\,\sin\theta\cos\theta\\
&= \uv z R^2 2\pi \left[ \frac{1}{2}\sin^2\theta\right]_0^{\pi/2} \\
&= \uv z R^2 2\pi \frac{1}{2}=\pi R^2 \uv z.
\endeq$$
1.62a
It's easiest to use the spherical form of the divergence to calculate this.
With $\myv v=\frac{1}{r}\uv r$, you will find that $\myv \grad \cdot \myv v=\frac{1}{r^2}$.
Next, the idea is to calculate separately the two integrals of the divergence theorem for a spherical volume $\cal V$ of radius $R$ bounded by a surface $\cal S$:
$$\oint_{\cal S} \myv v\cdot d\myv a = \int_{\cal V} \myv \grad \cdot \myv v\,d\tau.$$
For the function $\myv f(\myv r)=1/r^2$ these two integrals were *not* equal, which led us to believe that there could be a dirac delta function (at the origin). What about for this case? (If the two sides of the divergence theorem are equal, there's no need for a delta function. As a matter of fact, if there *were* an additional contribution from a dirac delta function, then the two integrals would not be equal after all.)
But for the first $\myv v$ given, you should find that both integrals are equal (value $4\pi R$) and so there is no need for a dirac delta function at the origin or elsewhere.
Chapter 4
HW #7
Problems: [4.1] 1, 3, 4, 6, 7
[4.2] 10, 11
Notes
In the last part: To fully ionize the atom, assume that you have to offset the nucleus, $d$, as far away from the center of the charge cloud as the radius of the atom, which we'll take to be that (Bohr) radius of the atom, which is half an angstrom. To do this, you'll increase the voltage difference between the plates, while keeping the separation (1 mm) between the plates the same.
show / hide
The induced dipole distance is $d/R=4.6\times 10^{-6}$.
The voltage necessary to ionize is approximately $10^8$ Volts.
Oh, it even includes the series expansion of the answer! Continuing to find $\myv E$:
$$\begineq
E(r)4\pi r^2 &=4\pi\frac{q}{\pi\epsilon_0 a^3}\left[ \frac{r^3}{3}-\frac{r^4}{2a}+... \right]\\
E(r) &=\frac{q}{\pi\epsilon_0 a^3}\left[ \frac{r}{3}-\frac{r^2}{2a}+... \right]
\endeq
$$
The lowest order term is $E(r)\approx\frac{q}{3\pi\epsilon_0 a^3} r$.
I won't show it, but the total of the cloud is $Q_\text{enc}(r\to\infty)=q$. So, the offset, $d$, between the nucleus and the center of the cloud for a particular electric field is $r$, that is, the dipole moment will be $p=qr$ so we have:
$$E(r)\approx\frac{1}{3\pi\epsilon_0 a^3} p.$$
So if $p=E\alpha$, apparently
the answer is $\alpha=3\pi\epsilon_0a^3$, which works out to about 1/7 of the empirical value in table 4.1.
In order for Eq 4.1 to hold, as $r\to 0$, $\rho$ should be a (non-zero) constant.
Torque on $\myv p_1$ is $\frac{2p_1p_2}{4\pi\epsilon_0r^2}$ pointing into the page.
Suppose the field inside a large piece of dielectic is $\myv E_0$, so that the electric displacement is $\myv D_0=\epsilon_0\myv E_0 + \myv P$.
b.) Now a small, needle-shaped cavity running parallel to $\myv P$ is hollowed out. (Fig 4.19b). Find the electric field at the center of the cavity in terms of $\myv E_0$ and $\myv P$. Also find the displacement at the center of the cavity in terms of $\myv D_0$ and $\myv P$.
[Assume that the cavities are small enough that $\myv P$, $\myv D_0$, and $\myv E_0$ in the dielectric are essentially uniform. Hint: Carving out a cavity is the same as superimposing an object of the same shape but opposite polarization.]
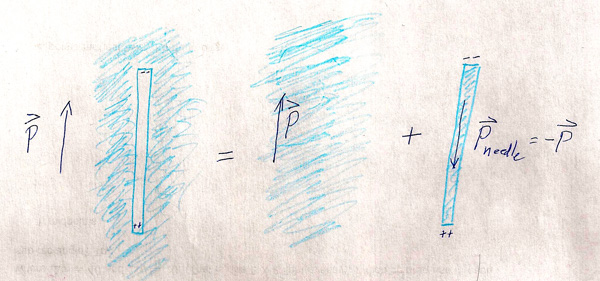
Since the polarization in the cavity is 0, the displacement at the center of the cavity is $\myv D=\epsilon_0\myv E+0=\epsilon_0\myv E_0$.
In the bulk of the dielectric, we had $\myv D_0=\epsilon_0\myv E_0+\myv P$. Solving this expression for $\epsilon_0\myv E=\myv D-\myv P$ and using it in the expression for $\myv D$, we find that the displacement at the center of the cavity is
$\myv D=\epsilon_0\myv E_0=\myv D_0-\myv P$.
c.) The thin wafer-shape will have a uniform charge density on the top and bottom surfaces given by $-\myv P\cdot \uv n$. The electric field between oppositely charged plates (like a capacitor) is something we've calculated before... (or use Gauss' Law to find it, assuming the field inside is uniform and pointing perpendicular to the plates.)
This is the problem with two slabs of different dielectrics, sandwiched between
the plates of a paralell plate capacitor.
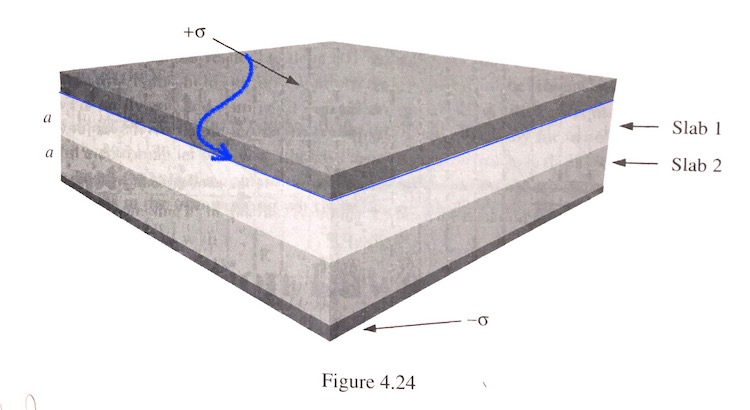
But the figure is a bit misleading: For example, the top plate of the capacitor is a conductor. So the free charge density (which arises due to the voltage difference between the plates) is not on the top of the plate, but on the inside surface--at the interface between the top conductur and slab 1.
Later on, you'll find the polarization in both slabs, and then, using $\myv P\cdot \uv n=\sigma_b$ you'll find the bound surface charge on various surfaces, including the top surface of slab 1.
So, the total surface charge at the interface of the top plate and the top of slab 1 is the sum of two contributions:
$$\sigma_\text{total}=+\sigma \text{ (the free charge) }+\sigma_b \text{ (bound charge on top of slab 1)}.$$
To figure $\myv D$, we only need to pay attention to the free charge, and the bound charge can be ignored.
$\myv D$ field lines start on positive free charge and end on negative free charge. So, the $\myv D$ field in the gap between the plates--even though it's filled with dielectric--will look very much like the $\myv E$ field between the plates of a traditional capacitor that has no material in the gap.
There is nothing to calculate. But you should make a sketch of the field lines between the plates (ignoring the dipole), and use that to justify your answer. Hints: What angle must the field lines make with the surface of each plate? Think about the dipole as made up of a positive and a negative charge.
Chapter 3
HW #6
[section 3.2] 6, 8
[section 3.3] 16, 18
Notes
The goal is to show that the average field inside a sphere of radius $R$ due to all the charge within the sphere, is
$$\myv E|\text{ave}=-\frac{1}{4\pi\epsilon_0}\frac{\myv p}{R^3}$$.
where $\myv p$ is the total dipole moment of the charge inside the sphere.
Remember how you averaged a function, $f(x)$ of one variable over an interval of length $L$:
$$\langle f(x) \rangle =\frac{1}{L}\int_a^{a+L} f(x)\,dx.$$
Similarly, to average a function of 3 variables over a volume, $V$:
$$\langle f(x,y,z) \rangle = \frac{1}{V} \iiint_V f(x,y,z)\,d\tau.$$
Or averaging over a spherical region, of radius $R$ centered on the origin, using spherical coordinates...
$$\langle f(r,\theta, \phi)\rangle = \frac{1}{\frac 43 \pi R^3}
\int_0^{2\pi}\int_0^\pi\int_0^R f(r,\theta,\phi)\,r^2\sin\theta\,dr\,d\theta\,d\phi.$$
Griffiths' breaks the problem down in pieces:
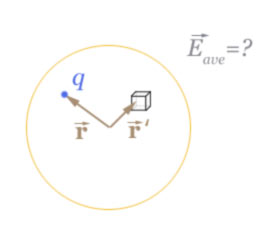Here, $\myv r\equiv$the position of a single, point charge $q$. We're interested
in finding the
average electric field inside a sphere as a function of the position $\myv r$.
So, we'll use $\myv r'$ to locate the
position where we evaluate the field $\myv E(\myv r')$ due to $q$, and
then integrate over positions $\myv r'$ inside the sphere, and then divide by the volume to get the average. The field at $\myv r'$
is proportional to $q/\rr^2$:
$$\myv E(\myv r')=\frac{1}{4\pi\epsilon_0}\frac{q(\myv r' -\myv
r)}{|\myv r'-\myv r|^3}.$$
Chapter 2
HW #3
1, 2, 3, 4, 5, 6
[2.2] 9, 10, 13, 14, 17, 18
Video homework
HW #4
HW #5
[2.5] 35, 36, 37, 38 [Capacitors] 39, 40, 48
Notes
d) Using the principle of superposition, think of this as [symmetrical arrangement from part c]
+ [charge of opposite sign at position of 'missing' charge]. So the net force
is that due to one opposite charge at the position of the hole.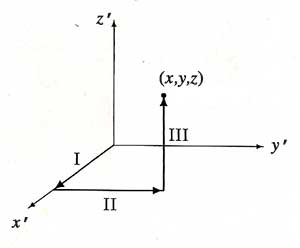
The origin is as convenient a starting point as any in this case.
I like to write the path integral in terms of primed and unprimed variables as
$$V(\myv r)=V(x,y,z)=-\int_{\myc{0,0,0}}^{\myc{x,y,z}}\myv E(x',y',z')\cdot d\myv l',$$
such that the answer comes out in terms of the unprimed coordinates.
$\int_I$:
Along this path, $d\myv l'=dx' \uv x'$, so the dot product will "pick out" just the $x'$ component of $\myv E$. Also, $y'=z'=0$, along this path.
So, $E_{x'}=ky'^2=k(0)^2=0$, and therefore,
$$-\int_I\myv E\cdot d\myv l' = -\int (0)dx'=0.$$
$\int_{II}$:
Along this path, $d\myv l'=dy' \uv y'$, so the dot product will pick out just the $y'$ component of $\myv E$.
Also, $x'=x$ and $z'=0$.
So, $E_y'=k(2xy'+(0)^2)=k2xy'$, and therefore,
$$-\int_{II}\myv E\cdot d\myv l' = -k\int_{y'=0}^y 2xy' \,dy'=-kxy^2.$$
$\int_{III}$:
Along this path, $d\myv l'=dz' \uv z'$, so the dot product will pick out just the $z'$ component of $\myv E$.
Also, $x'=x$ and $y'=y$.
So, $E_z'=k2yz'$, and therefore,
$$-\int_{III}\myv E\cdot d\myv l' = -k\int_{z'=0}^z 2yz' \,dz'=-kyz^2.$$
Putting these together:
$$\begineq V(x,y,z)&=-\int_I-\int_{II}-\int{III}\\
&=-k(xy^2+yz^2.\endeq$$
Test it by taking the negative gradient to see if you recover the original electric field:
$$-\myv \grad V = k(y^2\uv x+(2xy+z^2)\uv y+2yz\uv z).$$
Yes, this is $\myv E(\myv r)$!
All the charge on a circle is at the same distance
$\rr$ from point a, and distance $\rr'$ from point b. The radius of the circle is $r(\rr)=\rr/\sqrt 2$. So, the total charge $dq$ on the circle is
$$dq=\sigma 2\pi r\,d\rr=2\pi \rr\sigma\,d\rr/\sqrt 2.$$
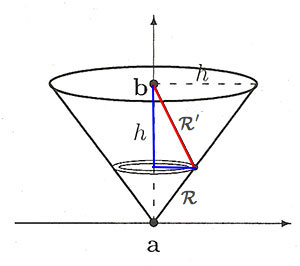we need to find $\rr'(\rr)$. Consider the colored right triangle. Pythagoras says:
$$\rr'^2=(h-r)^2+r^2=
\left(h-\frac{\rr}{\sqrt 2}\right)^2+\left(\frac{\rr}{\sqrt 2}\right)^2.$$
After expanding
$$\rr'=\sqrt{h^2-\sqrt 2h\rr+\rr^2}.$$
You can substitute this into the expression for $V(b)$ and we now have a (complicated) integral over $\rr$ to solve. The result (Mathematica!) is
$$V(b)=\frac{\sigma h}{2\epsilon_0}\ln(1+\sqrt 2).$$
Find the potential along $z$ from 0 to $R$. Using spherical symmetry, we expect that the potential at any distance $r$ is the same as what you find for $V(z=r)$.
You eventually need to solve an integral like this...
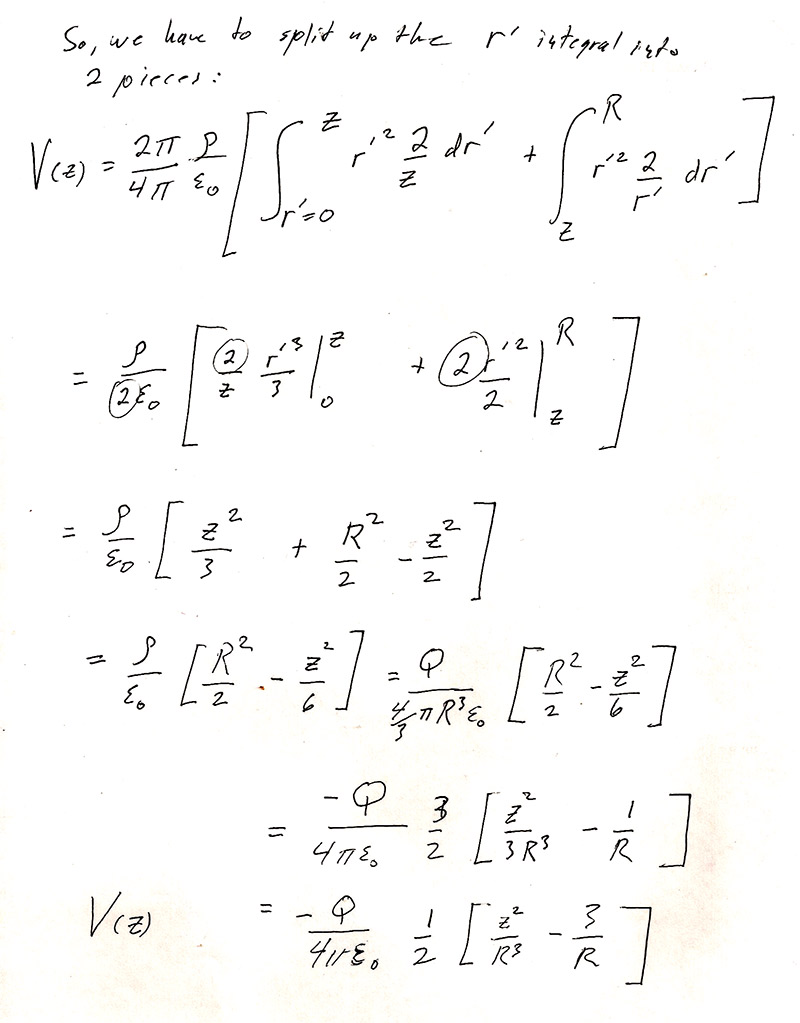
I realized afterwards it wouldn't have been that hard (though maybe hard conceptually) to just use $r$ and $\myv r$ instead of $z$ and $\myv r= z\uv z$. At any rate, this agrees with the answer to 2.21 which *is* in terms of $r$ rather than $z$.
b.) You can use Gauss' Law to calculate the electric field in any of the regions. In each region you found that $\myv E(r)$ is either 0 or $\frac{q}{4\pi\epsilon_0 r^2}\uv r$. Then, you can find the potential at 0 by integrating
$$\int_\infty^0 \myv E\cdot d\myv l$$
splitting the integral into appropriate segments.
The graph of the potential, $V(r)$, is continuous (though its first derivative does not have to be continuous) and it looks like this...
[The potential is graphed in units of $\frac{q}{4\pi\epsilon_0}$]
c.) Once the surface at $r=b$ is grounded ($V(r=b)\to 0$), there had better *still* be a net charge of $-q$ on the inner surface at $r=a$--that is $\sigma_a=-q/(4\pi\epsilon_0a^2)$, or else a Gaussian surface in between $a\lt r\lt b$ would enclose a net positive charge, and so $E_r$ could not be zero
inside
You know the expression for the pressure (force/area) acting on surface charge, pushing the surface charge--if it's on the surface of a conductor--away from the conductor. Use this to evaluate the force on a patch, $da$ of the surface.
show / hide
Or maybe, by now, you've started to recognize the pattern$\sin\theta\,d\theta = -d(\cos\theta)$, so you can say $u\equiv \cos\theta$ and solve $\int_{cos(\pi/2)=0}^1 u\,du=1/2$.
Let's say that there is a positive charge, $Q$, on a length, $L$, of the inner surface of the capacitor (with radius $a$). And there's a corresponding negative charge, $-Q$, in a length, $L$, on the outer surface, at radius $b$.
You can hopefully see that if $s\lt a$, or if $s \gt b$, the total enclosed charge is zero, so $\myv E$ is zero. The only region where the enclosed charge is *not* zero is $a < s < b$. And according to Gauss' law...
$$\begineq
\oint \myv E\cdot d\myv a &= Q_\text{enc}/\epsilon_0\\
E(s)\oint da =E(s)2\pi s L&= Q/\epsilon_0\\
\endeq$$
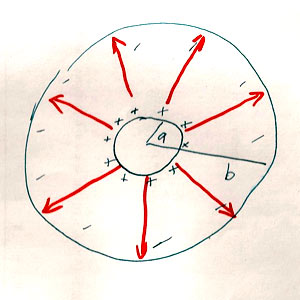And therefore $\myv E=E(s)\uv s=\frac{Q}{2\pi\epsilon_0L}\frac 1s$. Schematically (in cross section), with the electric field lines in orange (at right):
So, to calculate the potential difference between the two surfaces:
$$\begineq V(b)-V(a)&=-\int_a^b\myv E\cdot d\myv l \\
&=-\int_a^b E(s)\uv s \cdot ds \uv s=-\int_a^b E(s) ds \\
&=-\int_a^b \frac{Q}{2\pi\epsilon_0L} \frac 1s ds =-\frac{Q}{2\pi\epsilon_0L} \left(\ln s\right)_{s=a}^b\\
&=-\frac{Q}{2\pi\epsilon_0L} \ln \frac{b}{a}\\
\endeq
$$
This expression is correct. But notice that our path of integration has taken us from a location where the potential is high (for a positive charge) at $s=a$, ending at a location $s=b$ (with negative charge) where the potential is low. So $V(b)-V(a)$ will be negative. In order to get a positive potential difference, "$V$",
$$\frac{C}{L}=\frac{Q}{VL}=\frac{Q}{(V(a)-V(b))L}=\frac{Q}{\frac{Q}{2\pi\epsilon_0L} \ln \frac{b}{a}L\\}=\frac{2\pi\epsilon_0}{\ln\frac{b}{a}}.$$
a.) Assume that the charge density, $\rho(x)$, and the electric potential, $V(x)$, are functions of $x$ alone (no dependence on $y$ or $z$).
Chapter 1
HW #1
[1.2] 11, 12, 13, 15, 16, 18, 25, 27
HW #2
[1.4] 36, 37, 38, 39, 40, 42
[1.5] 43, 44, 45, 46a, 62
Notes
In the system translated in the $y$ direction by an amount $a$, the vector runs from the point $(0,-a,0)$ to $(l,m-a,n)$. Subtracting to find the components of $v$, we find still $v=\langle l,m,n\rangle$. The vector's components are unchanged by the translation.
But the cross product of the transformed vectors is
$-\myv A \times -\myv B =\myv A \times \myv B$ which is the *same* as the un-transformed cross product. So the cross product does not transform as a regular vector does under coordinate inversion. The cross product is a pseudo-vector, not a regular vector.
b) $\myv \grad f= 2xy^3z^4\uv x+3x^2y^2z^4\uv y+4x^2y^3z^3\uv z$
c) $\myv \grad f= e^2\sin y\ln z\uv x+e^x\cos y\ln z\uv y +e^x\sin y(1/z)\uv z$
b.) $h(-2,3)= 720 $ ft.
c.) Since $h$ is in feet and $x$ and $y$ are in miles, the units of partial derivatives like $\del h/\del x$ are feet / mile.
The gradient of $h$ is:
$$\begineq \myv \grad h &=\frac{\del h}{\del x}\uv x + \frac{\del h}{\del y}\uv y\\
&=10\left[ (2y-6x-18)\uv x + (2x-8y+28)\uv y\right]^{x=1; y=1}\\
&=10\left[ (2-6-18)\uv x + (2-8+28)\uv y\right]=-220\uv x +220\uv y
\endeq $$
So, the magnitude of the gradient (the steepest slope) is $\sqrt{2*220^2}=311$ ft/mile. And the direction of steepest ascent is equal units in the West and North directions, that is, towards the northwest.
a) $(\rr)^2=(x-x')^2+(y-y')^2+(z-z')^2$. So, the $x$-component of the gradient is:
$$\begineq
\uv x \frac{\del}
{\del x}(\rr)^2&=
\uv x \frac{\del}{\del x}[(x-x')^2+y\ \text{and }z\ \text{stuff}]\\
&=\uv x 2(x-x')\frac{\del x}{\del x} =\uv x 2(x-x')\endeq
$$
This is 2 times the x-component of $\myv \rr$, so we conclude that
$$\color{blue}\myv\grad\rr^2=2\myv r.$$
c) The answer is $\myv \grad \rr^n = n\rr^{n-1} \uv\rr$.
show / hide
b) $\myv \grad \cdot \myv v_b = y+2z+3x$
c) $\myv \grad \cdot \myv v_c = 0+2x+2y=2(x+y)$
d) Here you're supposed to find the Laplacian of
$$\myv v = x^2\uv x+ 3xz^2\uv y+-2xz \uv z.$$
The function is a *vector* function instead of a scalar. Use equation (1.43) to evaluate this:
$$\grad^2\myv v
= \left(\grad^2 v_x\right)\uv x +\left(\grad^2 v_y\right)\uv y
+\left(\grad^2 v_z\right)\uv z
,$$
where (one of these terms...):
$$\grad^2v_x = \frac{\del^2v_x}{\del x^2} +\frac{\del^2v_x}{\del y^2}
+\frac{\del^2v_x}{\del z^2}.$$
show / hide
b) $\grad^2T_b=-3T_b=-3\sin x\sin y \sin z$
c) Consider the scalar function
$$T_c=e^{-5x}\sin 4y\cos3z.$$
The Laplacian of this function is:
$$\grad^2 T_c
= \frac{\partial^2 T}{\partial x^2} +\frac{\partial^2 T}{\partial y^2}+\frac{\partial^2 T}{\partial z^2}.$$
Calculating each second derivative separately:
$$\frac{\partial^2 T}{\partial x^2} = (-5)(-5)e^{-5x}\sin 4y\cos3z=25 T_c.$$
$$\frac{\partial^2 T}{\partial y^2} = (4)(-4)e^{-5x}\sin 4y\cos3z=-16 T_c.$$
$$\frac{\partial^2 T}{\partial x^2} = (-3)(3)e^{-5x}\sin 4y\cos3z=-9 T_c.$$
Adding them up:
$$\grad^2 T_c = (25 -16 -9) T_c = 0$$
d) The answer is
$$\grad^2\myv v= 2\uv x+6x\uv y.$$
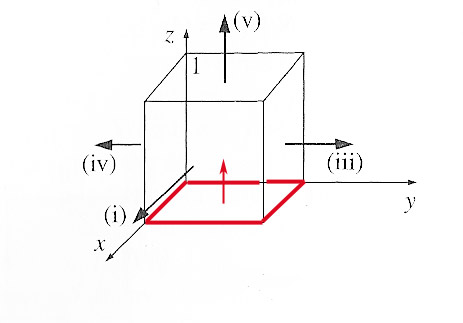
The flux going "down" through that face is +12. The total flux out of the box is then $$\Phi_\text{net}=20+12=32.$$
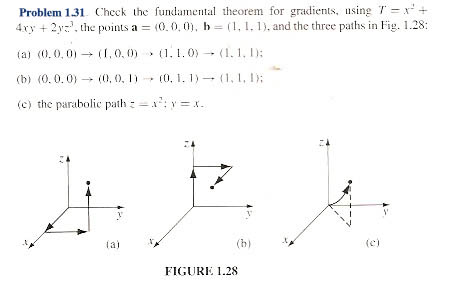
Along the 3rd line segment from $(1,1,0)$ to $(1,1,1)$ we have $d\myv l=dz\,\uv z$, and $x=1;\ y=1$. So
$$\begineq
\int\left(\myv \grad T\right)\cdot d\myv l
&=\int_{z=0}^{1}\left(\myv \grad T\right)_z\,dz\\
&=\int_{z=0}^{1}\left.\left( 6yz^2 \right)\right|^{x=1;y=1}\,dy\\
&=\int_{z=0}^{1}\left( 6\cdot 1 z^2 \right)\,dz=\left.2z^3\right|_{z=0}^{1}=2\\\endeq
$$
Adding these 3 together, we get...
$$\int_{(0,0,0)}^{(1,1,1)}\left(\myv \grad T\right)\cdot d\myv l = 1+4+2=7$$
Along the 3rd line segment from $(0,1,1)$ to $(1,1,1)$ we have $d\myv l=dx\,\uv x$, and $y=1;\ z=1$. So
$$\begineq
\int\left(\myv \grad T\right)\cdot d\myv l
&=\int_{x=0}^{1}\left(\myv \grad T\right)_x\,dx\\
&=\int_{x=0}^{1}\left.\left( 2x+4y \right)\right|^{y=1;z=1}\,dy\\
&=\int_{x=0}^{1}\left( 2x+4 \right)\,dz=\left.(x^2+4x)\right|_{x=0}^{1}=1+4=5\\\endeq
$$
Adding these 3 together, we get...
$$\int_{(0,0,0)}^{(1,1,1)}\left(\myv \grad T\right)\cdot d\myv l = 0+2+5=7$$
The parameter $t$ can be any convenient scalar. In this case, an easy way to describe the path is in terms of the single parameter $x$ where
$$\langle x(x),y(x),z(x)\rangle=\langle x,x,x^2\rangle,$$
This path starts at (0,0,0) and ends at (1,1,1) if $x$ runs from $0\to 1$. And the vector $d\myv l/dx$ is $\langle1,1,2x\rangle$.
Putting this together, we have...
$$\begineq \int \left(\myv \grad T\right)\cdot d\myv l &= \int_{x=0}^{x=1}
\left.\myc{2x+4y,4x +2z^3,6yz^2}\right|^{x=x; y=x; z=x^2}\cdot\myc{1,1,2x}\,dx
\endeq
$$
Work this from here. Hopefully the answer will match a) and b).
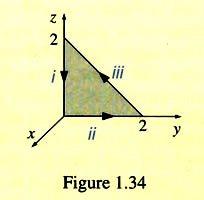
Along this path, the tangent vector is $dz\uv z$, but we'll start at $z=2$ and end at 0. Therefore $\myv v\cdot d\myv l=v_z\,dz=3zx\,dz$. But $x=0$ along the path, so $3zx=3z*0$, and the integral $\int_2^0 0\,dz=0$.
Along this path
the tangent vector is $d\myv l=dy \uv y$. Therefore $\myv v\cdot d\myv l
=v_y=2yz$. But since both $x=0$ and $z=0$ along the path, $v_y=0$. So the line integral along the path becomes:
$$\int_0^2 0\,dy = 0$$
The equation of the line that includes the hypotenuse is $y=2-z$.
The segment along the hypotenuse can be found by parameterizing the path. In terms of the parameter z, we can express it as $\myv l(z)=\myc{0,2-z,z}$ with $z$ ranging from $0\to 2$. Then, $d\myv l/dz=\myc{0,-1,+1}$ along the path.
The function itself is $\myv v=\myc{xy,2yz,3zx}$. Along the triangle's hypotenuse, $x=0$ and $y=2-z$, so $\left.\myv v\right|^{x=0;\ y=2-z}=\myc{0,2*(2-z)*z,0}=\myc{0,4z-2z^2,0}$.
So, we can write the integral along that segment:
$$\begineq
\int \myv v \cdot d\myv l
&=\int_{z=0}^2 \myv v \cdot \frac{d\myv l}{dz}\,dz\\
&=\int_{z=0}^2 \myc{0,4z-2z^2,0} \cdot \myc{0,-1,+1}\,dz\\
&=\int_{z=0}^2 (2z^2-4z)\,dz=\frac {16}{3}-8=-\frac 83\\
\endeq
$$
b.) This is that strange function $1/r^2$. You should find that the surface integral is $4\pi$ and the volume integral is $0$. The resolution of this is that the divergence of $\frac 1{r^2}\uv r$ is undefined at the origin. If we have it work like a delta function $4\pi \delta^3(\myv r)$, then the volume integral will formally give a result of $4\pi$.
Using the hint, we look at a vector
$\myv v=\myv c T=c_xT(x,y,z)\uv x+c_yT(x,y,z)\uv y
+c_zT(x,y,z)\uv z$,
which is the product of a constant vector $\myv c$ and a scalar field $T(x,y,z)$.
The fundamental theorem for divergences is our starting point:
$$\begineq \int_{\cal V}\myv\grad\cdot \myv v\,d\tau &= \oint_{\cal S}\myv v \cdot d\myv a\\
\int_{\cal V}\left(\frac{\del v_x}{\del x}+\frac{\del v_y}{\del y}+\frac{\del v_z}{\del z}
\right)\,d\tau &= \oint_{\cal S}\left(
c_xT\uv x+c_yT\uv y
+c_zT\uv z
\right) \cdot d\myv a\\
\endeq
$$
.
.
$$
\int_{\cal V}\myv \grad T
\,d\tau
= \oint_{\cal S} T(x,y,z) d\myv a$$
which is the result we are to show.
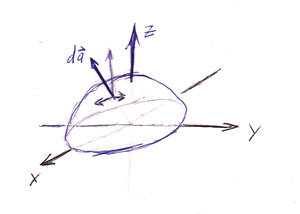Here, $d\myv a$ is a vector perpendicular to the surface of our half sphere (centered on the origin), that is in the radial direction $\uv r$:
$$d\myv a=dl_\theta\,dl_\phi\,\uv r=R^2\sin\theta\,d\theta\,d\phi\,\uv r.$$
Unfortunately, $\uv r$ is changing direction as you move around to different points on the surface of the sphere. So, you need to find the components of $d\myv a$ in a system in which the unit vectors are not changing direction, such as Cartesian coordinates.
Conceptually, you need to do 3 integrals, one each to find the $x$, $y$, and $z$ component of this integral.