Magnetic fields
Bring in compass, circuit to demo field of a current.
- Forces between currents
- Compasses show the local direction of magnetic field lines
- Cyclotron motion in a uniform magnetic field
- The Lorentz force - due to electric and magnetic field
- Current
- Charge conservation
Playing around with currents
When currents flow in parallel wires, forces arise. Watch this demonstration:
- Video of forces between current-carrying wires.
Summarizing the video: If two wires carry
- parallel currents $\Rightarrow$ the wires are attracted to each other,
- ...opposite currents $\Rightarrow$ the wires are repulsed by each other.
One thing that is *not* shown in the video is that a test charge close to the wires feels no force. That is...
$\Rightarrow$ This is not an electric force!
It's a magnetic force
Playing around with compasses
- An electric dipole in a uniform electric field experiences a torque.
- The equilibrium position of an electric dipole is parallel to the electric field lines.
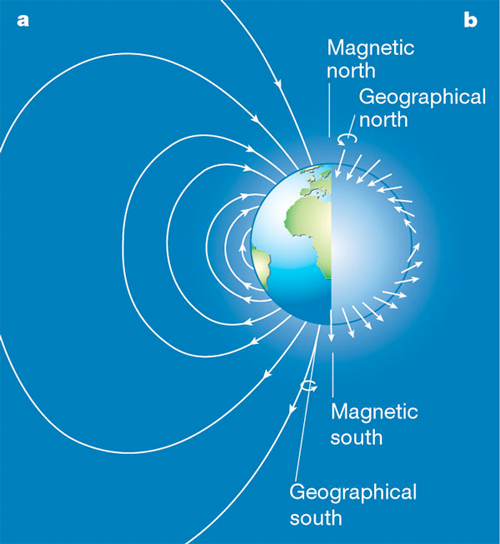
Compasses are small magnetic dipoles that, if allowed to pivot about their center, will line up parallel to magnetic field lines-- field lines for the magnetic field $\myv B$. Earth itself is a gigantic magnetic dipole (we're not completely sure why) with its axis aligned almost with Earth's axis of rotation. The component of Earth's field parallel to the surface points approximately North.
A compass placed close to a current-carrying wire points perpendicular to the wire.
Implying that there is a magnetic field perpendicular to the wire.
Explore Earth's magnetic field
Exploring Earth's magnetic field for a bit...
- Turn on the screen orientation lock on your phone.
- Pull up the PhyPhox app and select the magnetometer. It will detect the magnetic field at the location of your phone.
You'll see three graphs. Click on the $y$-component graph, and you'll be graphing the component of your local field in the direction parallel to your screen, from bottom to top.
- Hit the play button to start recording. Then hold your phone level, and turn around. What direction is your phone pointing when the y-field component is a maximum?
Lobster navigation
In a 2003 paper in Nature (NYTimes coverage) the authors showed that Caribbean spiny lobsters use Earth's field to make their way home.
Observations showed that spiny lobsters could wander far from home, and yet unerringly find their way back after dark.
The researchers applied a magnetic field from outside of a tank holding a lobster:
When we produced a magnetic field found at a location north of [their home], the lobsters walked south. And when we produced a field similar to one found at an area south of the site, they walked north.
Co-author Kenneth Lohmann
Field around a wire
By symmetry, you might expect the field to be radial.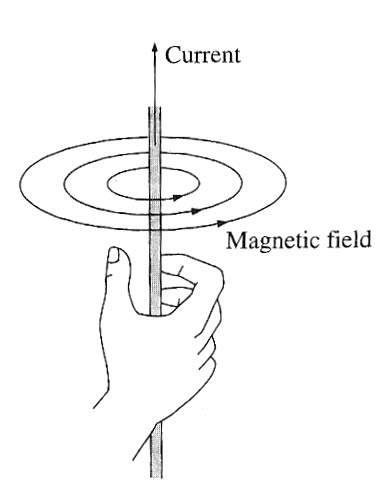 
pointing away from the wire. But as the compass deflection hints, it's a different kind of cylindrical symmetry: The field
curls around the wire.
Apparently the magnetic field, unlike the electric field...(a) has $\myv \grad \times$ curl and (b) does not apparently start or end on anything like a magnetic "charge"!
There's a right-hand rule to remember the direction of the field in relation
to the current.
The roundabout way of calculating this effect is to say:
Current $\Rightarrow$ Magnetic field $\Rightarrow$ Force on other moving charges
(OK, it's not *that* roundabout. This is very similar to what we did in electrostatics:
Charge $\Rightarrow$ Electric field $\Rightarrow$ Force on another charge ).
Experiments on the last link in the magnetic chain, "magnetic field $\Rightarrow$ force" can be summarized with this expression for the magnetic force on a moving charge: $$\myv F_\text{mag} = Q\,\myv v \times \myv B$$
Like other cross products, use a right-hand-rule to calculate the direction of the force:
- Fingers of the right hand straight out in the direction of $\myv v$,
- Curl those fingers towards $\myv B$ (make sure it's an angle < $180^o$), and
- Your thumb is pointing in the direction of the force.
Cyclotron motion
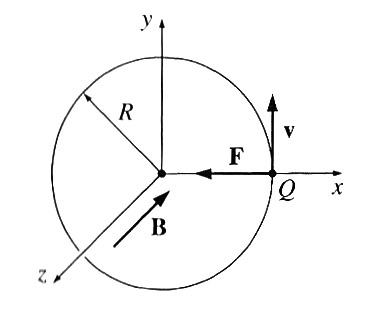
Particle with charge $Q$, mass $m$, $\myv v_0=v_0\uv y$.
Field everywhere the same: $\myv B=-B_0\uv z \perp \myv v_0$.
The particle will feel a magnetic force at right angles to its velocity, but won't be slowed down.
$\Rightarrow$ These are just the conditions for circular motion in the $xy$-plane, where the inward force $F_\text{mag}$ is just equal to $ma_\text{centripetal}$: $$|Q\myv v \times \myv B| = QvB = m \frac{v^2}{R}.$$
This corresponds to an angular speed (in radians/second) of
$$\omega_c = v/R = QB/m.$$
This is called the cyclotron frequency
.
What if the particle started out with an arbitrary velocity $\myv v$ that has some $z$-component to it? The force on the the particle would be: $$\myv F_{\text{mag }} =Q\myv v \times \myv B = -QB \myv v \times \uv{z}.$$
- $\Rightarrow \myv F_\text{mag} \perp \uv z$
- $\Rightarrow (\myv F_\text{mag})_z=0$
- There is no acceleration of the particle in the $z$ direction.
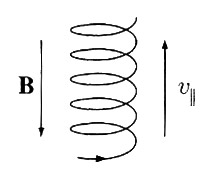With no change of the particle's momentum in the $\uv{z}$ direction, the particle
will tend to "corkscrew" around the direction of the magnetic field.
The 'solar wind' consists of ions & electrons emitted from the Sun. As these high-energy ions reach Earth and interact with Earth's magnetic field, if they spiral around magnetic field lines, where would they tend to enter Earth's atmosphere? show / hide answer:
As particles are "captured" on different field lines, (depending on their energy), they would tend to be deflected away from the equator, and follow field lines either towards the North or South magnetic pole.
This is the origin of the "Northern Lights" (Aurorara borealis) and the
"Southern Lights", (Aurora Australis)
Aurora Australis (Wikipedia). The Southern Lights encircle the continent of Antarctica, with Australia visible above and to the left.
You can *see* the light, because when
these ions hit the atmosphere, they knock into nitrogen
and oxygen molecules (majority of the atmosphere...), exciting them. Then, as these molecules return to their
ground state they give off light.
Mass spectrometer
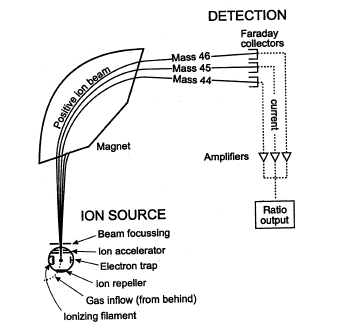
If several particles have the same velocity, the radius of their cyclotron
motion is proportional to their mass. The mass
spectrometer,
makes use of this to measure things like isotope ratios Carbon-13
/ Carbon-12 ratios for dating. Or Oxygen-16 / Oxygen-18 ratios for measuring
past temperatures.
Lorentz force
Putting the magnetic force together with the electric force, we get the Lorentz force law: $$\myv F = Q(\myv E + \myv v \times \myv B)$$
A puzzle: Work and magnetic forces
Work: $$dW= \myv F \cdot d \myv l$$ where the displacement is $$d\myv l=\myv v\,dt$$ is the displacement.
Since the magnetic force is alway perpendicular to the displacement of the moving charge, magnetic forces can do no work.
But what about those junkyard magnets--don't the iron objects rise through the air when you turn on the magnet? It seems like magnetic forces must be doing work there??
Read and summarize Griffiths' example 5.3 (on Moodle...) which addresses this puzzle.