Mechanics in a noninertial frame
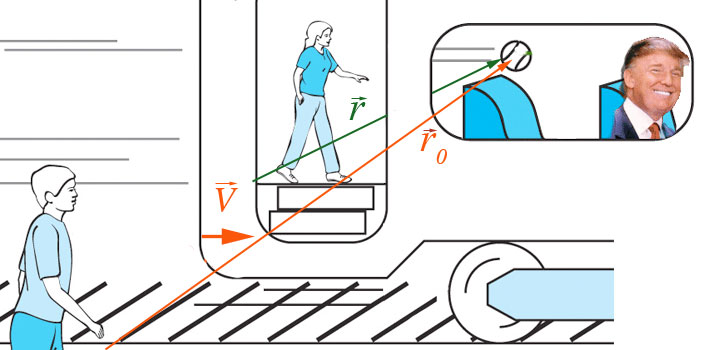
- ${\color{#c50} \mathscr{S}_0}$ is the reference frame of a stationary observer on the platform.
- $ \mathscr{S}_0 $ is an inertial frame
- ${\color{#c50}\myv r_0(t)}$ is a position vector in the $\mathscr{S}_0$ inertial frame, say, pointing at the CM of the baseball
Newton's law holds in $\mathscr{S}_0$: $$m\ddot{\myv{r}}_0 = \myv{F}$$
- ${\color{#060}\mathscr{S}}$ is a reference frame anchored in the train car.
- $\mathscr{S}$ is moving with velocity $\myv{V}(t)$ according to the inertial frame.
- It might be an accelerating, non-inertial frame.
- ${\color{#060}\myv r(t)}$ is the position vector of the same ball wrt to the origin of $\mathscr{S}$.
If we add the velocities according to Galilean relativity (slow compared to $c$, so non-relativistic): $$\dot{\myv{r}}_0= \dot{\myv{r}} + \myv{V}.$$
Differentiating, and rearranging $$\ddot{\myv{r}}=\ddot{\myv{r}}_0 - \myv{A}$$
Multiplying through by $m$, and identifying $m\ddot{\myv{r}}_0=\myv{F}$ $$m\ddot{\myv{r}} = \myv{F}-m\myv{A}$$
From the point of view of an observer in $\mathscr{S}$ then, it looks like Newton's 2nd law still works as long as we add in an extra term sometimes called the inertial force:
Inertial force: $$\myv{F}_\text{inertial} \equiv -m\myv{A}.$$
This force viewed in $\mathscr{S}$ is opposite the acceleration of the noninertial frame, as viewed in $\mathscr{S}_0$.
Example
Re-prising Problem 7.22: The elevator accelerating with acceleration $\myv{a}$ upwards. What is the period of a pendulum suspended from the ceiling?
This time, we can easily write down the extra inertial force in the elevator's frame, which is $\myv{F}_\text{in} = -mA \uv{z}$. This just adds together with the gravitational force $-mg \uv{z}$, to give a net force on the pendulum bob of $-m(g+A)\uv{z}$. The angular frequency will be $\omega=\sqrt{(g+A)/L}$.
[The answer to problem 7.22 is that the equation of motion of motion is: $$L\ddot \phi=(g+a)\sin\phi.]$$
The Tides
How many high tides per 24 hours?
Tide Info from NOAA: North Carolina.
$\Rightarrow$ Our analysis should lead to ~two tides per day
Tides in the Bay of Fundy:


[minute physics explains it in 10 seconds...]
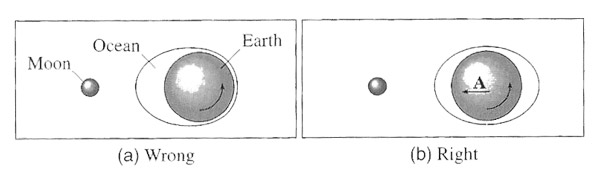
Since Earth and the Moon are rotating around each other, we can think of Earth as continuously "falling" (having an acceleration) towards the Moon with an acceleration equal to the force of gravity acting along the line that connects Earth and the Moon which is... $$\myv{A} = -GM_m\frac{\myv{d}_0}{d_0^3}$$

A mass $m$ which is at rest with respect to the accelerating Earth at a position as shown is subject to these forces:
- The force of Earth's gravity $m\myv{g}$ acting along $-\myv{r}$,
- the force of the Moon's gravity: $-GM_mm\frac{\myv{d}}{d^3}$,
- the sum of any other non-gravitational forces from its environment acting on it that we'll call $\myv{F}_{ng}$, and finally
- the inertial force which is $-m\myv{A}$ with the expression for $\myv{A}$ above.
This results in an equation of motion $m\ddot{\myv{r}}=m\myv{g} -GM_mm\frac{\myv{d}}{d^3} + \myv{F}_{ng} + GM_mm\frac{\myv{d}_0}{d_0^3}.$
The two terms which depend on the Moon's mass we'll call the tidal force:
$$\myv{F}_{tid} = -GM_mm\(\frac{\myv{d}}{d^3} - \frac{\myv{d}_0}{d_0^3}\).$$
The net effect is...
[Sketch the two contributions, and the net $\myv{F}_\text{tid}$ at Earth's surface at 12, 3, 6, and 9 "o'clock" on the diagram below.]

Tide height
Read up on the Lagrangian points.
Mathematical stretching:
If $x\ll 1$, then a Taylor expansion of $f(x)=(1+x)^p$ (where $p$ is some constant) around $x=0$ should be a very good approximation to $f(x)$. Write out the first 3 terms of the Taylor expansion.
We'll try to find the shape of the tidal surface by:
- arguing that the water surface should be co-incident with an equipotential surface of the potential.
- But, ummm, of what potential?
- We'll re-write the forces in terms of the gradient of an effective potential,
- And then find the height difference between the highest and lowest points on the equipotential surface.
This is not a stable configuration for the top surface of a pond on the surface of the earth:

How can we find the shape of the surface of the pond?
The water could lower its total gravitational potential energy by re-arranging itself until.... its top surface was coincident with an equipotential surface of ...what?
Perhaps we should think in terms of a test mass just above where we think the surface of the water is. We can calculate the gravitational potential energy of such a test mass at each point of some 'test surface', then we've mapped out one equipotential. By means of this trick, we try to argue about the shape of the surface without having to worry about the details of the pressure and or any other forces acting within the body of water: We say, the shape of the surface is going to be an equipotential of the potential from which all the external forces acting on a test chunk of water are derived.
Let's apply the same argument about the top surface of the water aligning with an equipotential surface to find the variation in tide height for the earth-moon system. Neglecting the "non-gravitational" force, the other forces acting on a a test mass 'm' near the surface of the earth are: $m\ddot{\myv{r}}=m\myv{g} -GM_mm\frac{\myv{d}}{d^3} + GM_mm\frac{\myv{d}_0}{d_0^3}.$
The forces on the right are all conservative and so can each be expressed as $\myv{f}=-\myv{\grad}U$.
The force due to Earth's gravity can be derived from a potential that depends on the height above the surface of the earth: $U_{e}= mgh$.
The second term is the inverse-square force of the moon's gravity and can be derived from $U_m = -(GM_mm)/d$.
The last term is a constant vector always pointing to the right (the $\uv{x}$ direction), so the corresponding effective potential is $U_{i n} = -GM_mm(x/d_0^2)$.
The gradient of these second two terms together gives the tidal force, so let's call $U_{tid} = U_m+U_{i n}$.
So, let's set $U(Q)=U(P)$ in the diagram below.

This means $$U_{e}(P)-U_{e}(Q) = mg\Delta h = U_{tid}(Q)-U_{tid}(P),$$
where $\Delta h$ is precisely the height difference between low and high tide we're looking for.
At 'Q'$, $x=0$ so $U_{in}(Q)=0$, and we only need to calculate the $U_m$ part of the tidal potential: $$\begineq U_{tid}(Q)&=&U_m(Q) = -\frac{GM_mm}{d}\\ &=& -\frac{GM_mm}{\sqrt{d_0^2+R_e^2}} \\ &=& -\frac{GM_mm}{d_0} \left(1+\frac{R_e^2}{d_0^2}\right)^{-1/2}\endeq$$
Our Taylor expansion yields $(1+\epsilon)^p=1+p\epsilon+...$. With the power -1/2 in the equation above, and $(R_e/d_0)^2 \ll 1$, this becomes... $$U_{tid}(Q) \approx -\frac{GM_mm}{d_0}\left(1-\frac{R_e^2}{2d_0^2}\right).$$
At 'P', $d=d_0-R_e$ and $x=-R_e$, so $$\begineq U_{tid}(P) &=& U_m(P)+U_{in}(P)\\ &=&-GM_mm\[\frac{1}{(d_0-R_e)} -\frac{R_e}{(d_0)^2}\].\endeq$$
We can simplify this writing $1/(d_0-R_e)=\frac{1}{d_0}(1-(R_e/d_0))^{-1}$. Doing a Taylor expansion of $(1-\epsilon)^{-1}$ and keeping three terms, one will cancel out the inertial term, (problem 5) and you're left with
$$U_{tid}(P) \approx -\frac{GM_mm}{d_0}\left(1+\frac{R_e^2}{d_0^2}\right)$$
Substituting these into (11) and solving for $\Delta h$, using along the way that $g=GM_e/R_e^2$, we end up with
$$\Delta h = \frac{3 M_m R_e^4}{2M_e d_0^3} = 54 cm \approx 1.7 {\rm feet}.$$
The same calculation using the greater distance, but also greater mass of the Sun yields $\Delta h=25cm$. Taking into account that the Sun and Moon are sometimes lined up, and sometimes at right angles, it seems our overall tide height difference should be somewhere between:
$54-25=$19 cm < $\Delta h$ < 79 cm $=54+25$ cm.
Does this jibe with the current North Carolina tides? With the Bay of Fundy or Lake Michigan?
One last tide puzzle

According to our picture, high tide should occur when the moon is either directly overhead or at "lunar midnight" when it's exactly on the opposite side of the earth.
How long does it take for the Moon to circle Earth once? So, in this time, we should see how many maxima / minima? Here is one month of tide data
Based on the current height difference of the tides, do you think that Moon / Earth / Sun are all mutually aligned or pretty far mis-aligned?
Check observations:
- North Carolina tides, times and heights (NOAA).
- Moonrise / Moonset times for Durham, North Carolina.
Are these in agreement with the picture??
See Merlot, Butikov: there is a resonance with $\omega_0 \ll \omega_{\text drive}$. How long do you think it would take a wave to travel around the world at the equator?
Water in a spinning container


Turn on the turntable and wait until the water is rotating with the jar (that is, water is still relative to the jar).
What's the profile of the surface of the water?
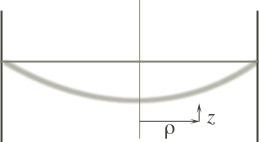
Let $\mathscr{S}$ be a noninertial frame of reference a distance $\rho$ from the center of rotation. This frame of reference has acceleration $A=v^2/\rho$ directed horizontally towards the center of rotation.
Then, the equation of motion for a small mass of water in $\mathscr{S}$ is $$m\ddot{\myv{r}} =-mg\uv{z} + \myv{F}_{in}=-mg\uv{z} + m(v^2/\rho) \uv{\rho} = -mg\uv{z}+m\omega^2\rho\, \uv{\rho}.$$
The gravitational force is $-\myv{\grad}U$ where $U=mgz$. What should we use to generate this other, centripetal term? Can you come up with a $U_{eff}$?
We'd expect the water to come to rest in the noninertial frame in such a way as to minimize the total potential energy. That is, the top surface should be coincident with some equipotential surface given by: $$U=C o n s t = U_g + U_{eff} = mgz+U_{eff}$$
Dividing the constant by $m$ just gives a different constant, so the equipotential surface profile should obey $$z = U_{eff}/(mg) + C o n s t$$
What equation does this give you for the shape of the cross-section of the water surface?
Homework
Chapter 9, problems: 2, 5