Line Integrals

Line integral
Area of the wandering, irregular fence...
Consider the smooth curve, $C$, in the $x$-,$y$-plane described by the vector function parameterized in terms of $t$
$$\myv r(t)=\langle x(t),y(t)\rangle.$$

If the curve is chopped up into $n$ arcs...
The line integral of $f$ along $C$ is: $$\int_C f(x,y)\,ds=\lim_{n\to\infty} f(x_i^*,y_i^*)\Delta s_i.$$
In section [10.3]--arclength--we found that...
- $\myv r'(t)=\langle x'(t),y'(t) \rangle$ is a vector tangent to the curve.
- [If the parameter $t$ is time, then $\myv r'(t)$ is the velocity vector.]
- The arclength distance traversed when $t$ changes by $\Delta t$ is $$\Delta s\approx |\myv r'|\Delta t=\sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 }\Delta t$$
$$\int_Cf(x,y)\,ds = \int_{t=a}^b f(x(t),y(t)) \sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 } \,dt.$$
Example
 $\int \frac yx\,ds$
along the line $x=t^4$, $y=t^3$, $0\leq t \leq 1$.
$\int \frac yx\,ds$
along the line $x=t^4$, $y=t^3$, $0\leq t \leq 1$.
$$\begineq \int_C \frac yx\,ds &= \int_{t=0}^1 \frac {y(t)}{x(t)} \sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 } \,dt\\ &= \int_{t=0}^1 \frac {t^3}{t^4} \sqrt{ \left( 4t^3\right)^2+\left(3t^2\right)^2 } \,dt\\ &= \int_{t=0}^1 \frac {1}{t} \sqrt{ 16t^6+9t^4 } \,dt\\ &= \int_{t=0}^1 t \sqrt{ 16t^2+9 } \,dt\\ \endeq $$
Substitution of variables: $u=16t^2+9$, so $du=32t\,dt$:
$$\begineq \int_C \frac yx\,ds &= \frac{1}{32}\int_{u(0)}^{u(1)} \sqrt{ u } \,du\\ &= \frac{1}{32}\left[ \frac 23 u^{3/2} \]_9^{25} = \frac{1}{16*3}(125-27)=\frac{49}{24} \endeq $$
Example
$$\int_C(x+y^2)ds$$ where $C$ is the line from $(0,0)$ to $(3,0)$.
- Along this line, $y=0$ so $x+y^2\to x$.
- $C$ is along the $x$-axis. Let's use $x$ as our parameter.
- Along the $x$-axis $ds=dx$.
$$\int_C(x+y^2)ds = \int_{x=0}^3x\,dx = \frac 92.$$
Example
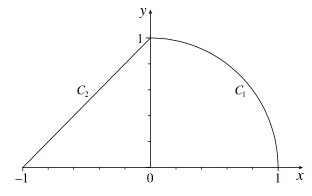 $\int (x+y)\,ds=?$
$\int (x+y)\,ds=?$
This can be split into two integrals...
Let's do the integral over $C_1$ in polar coordinates with the parameter $\theta$.
- $x=r\cos\theta;\ \ y=r\sin\theta$
- Arclength $$\begineq ds&=\sqrt{ \left(\frac{\del\, r\cos\theta}{\del\theta}\right)^2 + \left(\frac{\del\, r\sin\theta}{\del\theta}\right)^2 }\,d\theta \\ &=\sqrt{ \left(-r\sin\theta \right)^2 + \left(r\cos\theta\right)^2 }\,d\theta \\ &=r\,d\theta \endeq $$
- $r=1$
Putting these pieces together, $$\int_{C_1} (x+y)\,ds =\int_{\theta=0}^{\pi/2}\left( \cos\theta + \sin\theta \right)\,d\theta=2.$$
Along $C_2$: The equation of the line is $y(x)=x+1$. Let's use $x$ as our parameter... $$ds=\sqrt{ \left(\frac{\del x}{\del x}\right)^2+\left(\frac{\del(x+1)}{\del x}\right)^2 }dx=\sqrt 2\,dx$$
$$\begineq \int_{C_1} (x+y)\,ds &= \int_0^1 (x+(1+x))\sqrt 2\,dx\\ &=\sqrt 2 \int_0^1 (1+2x)\,dx=\sqrt 2\left[ (x+x^2)\]_0^1=2\sqrt 2. \endeq $$
Which way?
Does it matter which way you traverse the path? Should it matter? ...
An increment of arclength, $ds$, is always positive, so $$\int_{-C}f(x,y)\,ds = \int_C f(x,y)\,ds$$
Line integrals - 3D
$$\begineq \int_Cf(x,y,z)\,ds&=\int_{t=a}^bf(\myv r(t))\,dt\\ &=\int_a^bf(x(t),y(t),z(t))\sqrt{ \left(\frac{\del x}{\del t}\right)^2+\left(\frac{\del y}{\del t}\right)^2 +\left(\frac{\del z}{\del t}\right)^2 }\,dt \endeq $$
To Do
- Scalar line integrals
Force fields and line integrals
 Hollywood version of a force field...
Hollywood version of a force field...
The more common version is the force of gravity (close to Earth's surface): $$\myv F_g=-mg\uv k$$ or the electric force on a particle with charge $q$ in an electric field $\myv E$, which is $$\myv F_e = q\myv E(x,y,z)$$
The work, $\Delta W$, (units of energy) done by a force, $\myv F$ on a particle is only non-zero if the particle moves a distance $\Delta \myv s$: $$\Delta W = \myv F \cdot \Delta \myv s$$
In a force field the force acting on a particle, $\myv F=\myv F(x,y,z)$, depends on position.
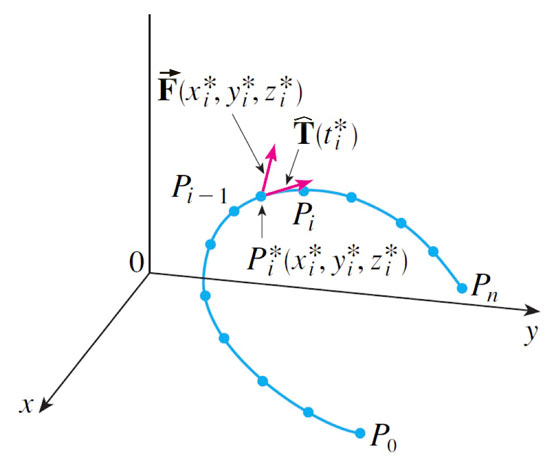 A particle moves along the curve $C$ specified by $\myv r(t)$ shown.
The work done by the field is
$\Delta W_i=\myv F(x_i,y_i,z_i)\cdot\myv \Delta \myv s_i$, so...
$$W\approx\sum_{i=1}^n\myv F(x_i^*,y_i^*,z_i^*)
\cdot\uv T(x_i^*,y_i^*,z_i^*)\Delta s_i$$
where $\Delta s_i$ is the distance moved in interval $i$, and $\uv T$ is the unit tanget vector.
A particle moves along the curve $C$ specified by $\myv r(t)$ shown.
The work done by the field is
$\Delta W_i=\myv F(x_i,y_i,z_i)\cdot\myv \Delta \myv s_i$, so...
$$W\approx\sum_{i=1}^n\myv F(x_i^*,y_i^*,z_i^*)
\cdot\uv T(x_i^*,y_i^*,z_i^*)\Delta s_i$$
where $\Delta s_i$ is the distance moved in interval $i$, and $\uv T$ is the unit tanget vector.
In the limit $n\to\infty$ the sum becomes an integral, the line integral of $\myv F$ along $C$: $$W=\int_C\myv F\cdot\uv T\,ds=\int_C \myv F\cdot d\myv r = \int_{t=a}^b\myv F(t)\cdot \myv r'(t)\,dt.$$
Positive, zero, negative dot products
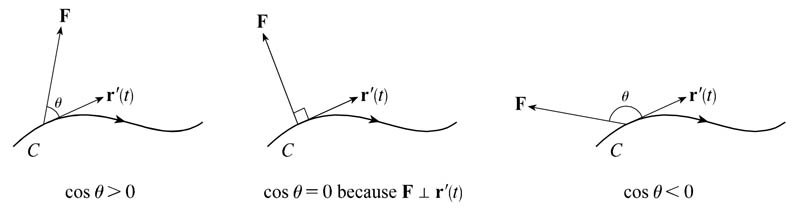
Positive, negative, or zero?
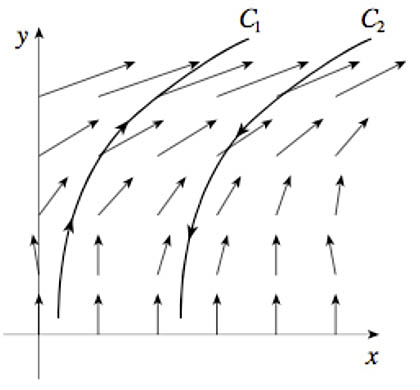 $\int_{C_1}\myv F\cdot d\myv r\ \ $?
$\int_{C_1}\myv F\cdot d\myv r\ \ $?
$\int_{C_2}\myv F\cdot d\myv r\ \ $?
Example
Find the work done by the vector force field $$\myv F = (y-x^2)\uv i + (z-y^2)\uv j +(x-z^2)\uv k$$
 ...over the oriented curve
...over the oriented curve
$\myv r(t)=t\uv i +t^2\uv j+t^3\uv k$
from $(0,0,0)$ to $(1,1,1)$.
$$W=\int_{t=0}^1\myv F(t)\cdot \myv r'(t)\,dt.$$
Example
Find the work done by the vector force field $$\myv F = x\uv i +z \uv j + y\uv k$$
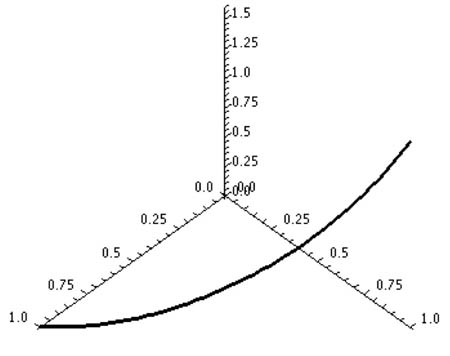 ...over the oriented curve
...over the oriented curve
$\myv r(t)=\cos t \uv i +\sin t \uv +t\uv k$
for $0\leq t \leq \frac\pi 2$.
$$W=\int_{t=0}^0\myv F(t)\cdot \myv r'(t)\,dt.$$
Line integral in differential form
$$\myv F(x,y,z)=P(x,y,z)\uv i +Q(x,y,z)\uv j +R(x,y,z)\uv k.$$
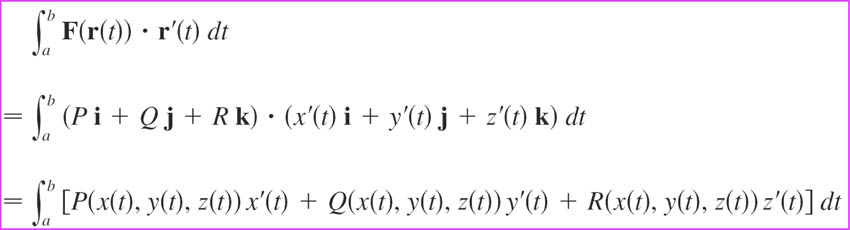
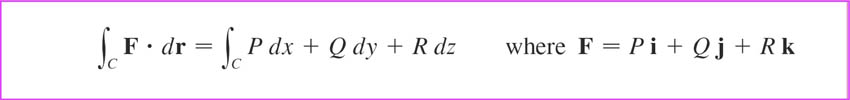
Example
$$\myv F(x,y)=x\uv i+x^2\uv j.$$
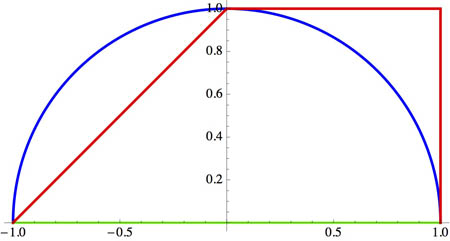 Three paths from $(-1,0)$ to $(0,1)$.
Three paths from $(-1,0)$ to $(0,1)$.
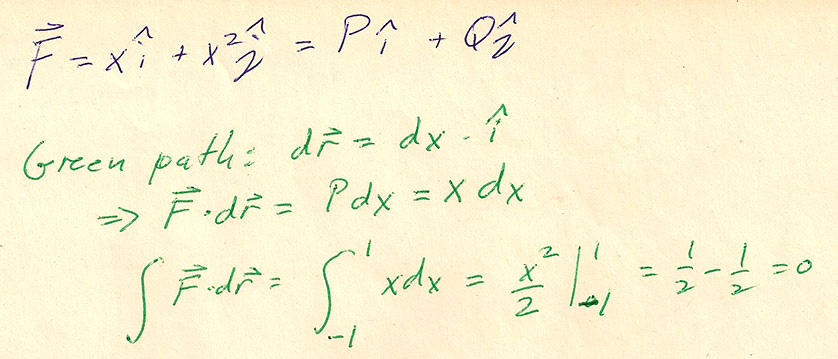

Corrected 19 May: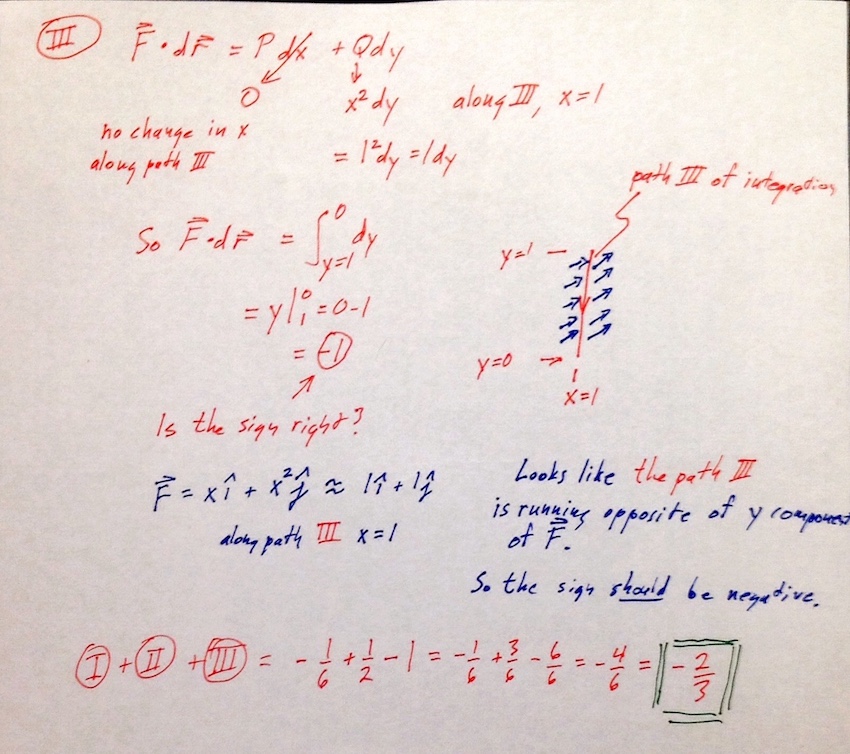

To Do
- Group work 2: Computing Vector Line Integrals