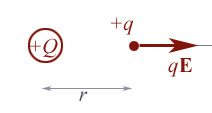
Electric potential

Reading: Chapter 23, ELECTRIC POTENTIAL

Study guide: Chapter 24

Topics:

1. Electric potential $V$--a scalar--which we derive from work.
   1. Potential of point charge(s)
   2. Superposition of scalars, not vectors
2. Equipotentials and field lines
3. Electrostatic potential energy
   1. of a system of charges
   2. of a continuous charge distribution
4. Electric field as the gradient of $V$

Energy

The gravitational force between two point masses is $\propto 1/r^2$ and is conservative (can be derived from a potential energy), so it seems reasonable that since the electric force between two point masses $\propto 1/r^2$, that it too should be conservative, and can be derived from a potential energy. We'll find this energy by integrating the dot product of force and displacement: $dW=\int \myv F\cdot d\myv l$.

A small test charge $q$ in the field of a source charge $Q$ at origin feels a force $$\myv F = k\frac{qQ}{r^2}\uv r.$$

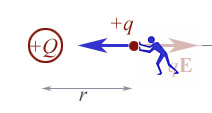But if an external agent (let's call him "Joe") pushes on the charge, he exerts a force exactly opposite to the one the charge feels.

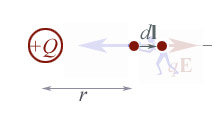Consider the work done when moving the charge by $d\myv l$ from $x=r$ to $x=r+dl$. Is it $dW= qE\,dl$ or $dW= -qE\,dl$?

Well, what both points of view could perhaps agree on is that when two like charges are further apart, there is a lower potential energy. In the picture, $\myv E$, and $d\myv l$ are both pointing in the positive $\uv x$ direction, so $\myv E \cdot d\myv l \gt 0$. So, to make the change in energy come out right, we need to have

$$ U(\myv b)-U(\myv a)= -\int_{\myv a}^{\myv b}q\myv E\cdot d\myv l.$$

Two points of view are possible, though the potential remains the same:

• Joe had work done on him (negative work), when he backed up, or
• "The field" did work on (positive work) the charge (and Joe) to push it away.

Now, the electric potential (just like E vs F) is some characteristic of space that depends only on the source charges and not the test charge: $$\begineq\Delta V&\equiv&\frac{\Delta U}{q} = -\frac{1}{q}\int q\myv E\cdot d\myv l\\ &=& -\int \myv E \cdot d\myv l.\endeq$$.

[Electric field between 2 flat plates with a potential difference of 10 V separated by 2 mm? We will shortly see that the electric potential (watch out for just "potential"!) on a conductor is everywhere the same....]

Potential of a point charge

In polar coordinates, the position of our test charge is $(r,\phi)$. But for the field $\myv E(\myv r)=E_r(r)\,\uv r$ of a point charge, the dot product depends *only* on the distance $r$ and not the angle $\phi$, so $$\begineq \Delta V = V(\myv b)-V(\myv a) &=& -\int_a^b q\myv E(\myv r)\cdot d\myv l = -\int_{\myv a}^{\myv b} \frac{kQ}{r^2}\,dr\\ &=&+kQ\[\frac{1}{r_b}-\frac{1}{r_a}\].\endeq$$

What is the reference point for potential? It's arbitrary...all we can measure is differences in the potential between two points. So we will define the reference location to be $V(r=\infty)=0$. So, to calculate the potential near a point charge $Q$ we set

• Our starting position at the reference location $r_a=\infty$ so $V(\myv a \to \infty)=0$,
• Our ending position at $\myv b$ so let's call $r_b=r$,

$$\Rightarrow V(\myv r) = \frac{kQ}{r}.$$

Two particles and conservation of energy

A positron (anti-electron) is moving at a speed of $6 \times 10^6$ m/s towards a far-off, slow-moving $\alpha$ particle. What is the closest the two particles can get to each other?

Superposition

Many particles instead of just one? Think about integrating the net electric field from point charges...

$$\begineq V(\myv r) - V(\infty) &=& -\int_\infty^{\myv r} \myv E_\text{net}(\myv r)\cdot d\myv l \\ &=&\int_\myv{r}^\infty \myv E_\text{net}(\myv r)\cdot d\myv l\\ &=&\int_\myv{r}^\infty \left(\myv E_1(\myv r)+\myv E_2(\myv r)+\myv E_3(\myv r)+...\right)\cdot d\myv l\\ &=&\int_\myv{r}^\infty\myv E_1(\myv r)\cdot d\myv l+\int_\myv{r}^\infty \myv E_2(\myv r)\cdot d\myv l+\int_\myv{r}^\infty\myv E_3(\myv r)\cdot d\myv l+...\\ &=& V_1(\myv r) + V_2(\myv r) +V_1(\myv r) +...\\ V(\myv r) &=& \frac{kQ_1}{r_1} + \frac{kQ_2}{r_2} + \frac{kQ_3}{r_3} + ...\endeq$$

Where $r_3$ is the distance from charge 3 to $\myv r$, etc.

[Find the potential on the perpendicular bisector between two point charges...]

[You can also do integrals...]

Conductors

Show that all the points in a conductor must be at the same potential by integrating the field from $a$ to $b$.

Two methods

$V=\int_\myv{r}^\infty \myv E\cdot d\myv l$ and $V=\sum \frac{kQ_i}{r_i}\to\int \frac{k\,dQ}{r}$.

Multivariate vector calculus

Aw, Let's just go hiking instead!

Earth's landscape is actually an energy landscape: Gravitational potential energy = $mgh$. So, the earth's landscape is a "graph" of $U \propto h$ where $U(x,y)$ is a function of two coordinates.

Partial derivatives

On a contour map of the landscape, points of equal height (equi-height-als) are connected by contour lines.

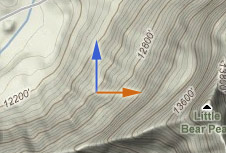$\frac{\del h}{\del x}\equiv$ slope (change in height 'rise' / 'run') as you move east (no change in north/south direction). Is this positive or negative in the picture?

$\frac{\del h}{\del y}\equiv$ slope as you move north (with no change in the east/west direction). Is this positive or negative in the picture?

[If $h(x,y)=13y^2(x^2-1)$, what is the slope in the $x$-direction at (2,1)? That is... $\del h/\del x$?]

See these visualizations of partial derivatives and directional derivatives.

Direction of greatest slope

How would you figure out in which direction the slope is greatest?
It ought to be somewhere between:

• east - the direction that the height was increasing for $x$-motion, and
• south, a.k.a. $-\uv y$: the direction that the height was increasing for $y$-motion, since the slope was negative when we moved north.

We also probably ought to weight the direction more towards either $x$ or $y$ depending on which slope (partial derivative) was greater.

So, how about...

$$\frac{\del h}{\del x} \uv{x} + \frac{\del h}{\del y} \uv{y} \equiv \myv{\grad} h.$$ The gradient.

This vector, the gradient turns out to have all of these characteristics:

• points in the direction of greatest increase of the height,
• its magnitude is the steepest slope out of all directions away from that point.
• it points perpendicular to the contour line at that point on the map.

Skiers talk about a "fall line"-the direction of steepest descent,

or the direction that water would flow away from a particular point on the mountainside. $-\myv{\grad} U$ points in the direction of the fall line. (Though, if we're picky, it doesn't actually point "down" the mountain slope, only points in the same $x$-, $y$-direction of the fall line, but with no $h$-component).

Change of height

If we start hiking, by how much will our altitude $h$ change? Call the change $dh$. The change of height will depend on...

[As long as we take small steps, the slope is not changing very much.]

• how far we move towards (or away from) the east, $dx$,
• how far we move towards the north, $dy$,
• the slopes in the easterly and northerly directions: $\frac{\del h}{\del x}$, $\frac{\del h}{\del y}$.
  

$$dh=\frac{\del h}{\del x}dx+ \frac{\del h}{\del y}dy=\myv \grad \cdot d\myv l.$$ Since $d\myv l = dx\,\uv x + dy\, \uv y+ dz\, \uv z$.

Now, apply this to....$$V=-\int \myv E \cdot d\myv l$$ where the displacement $d\myv l = dx\,\uv x + dy\, \uv y+ dz\, \uv z$

....

We conclude that $$\myv \grad V = \myv E$$

and in terms of components... $$E_x = -\frac{\del V}{\del x}$$ $$E_y = -\frac{\del V}{\del y}$$ $$E_z = -\frac{\del V}{\del z}$$

[Find the direction, approx magnitude of the electric field from a contour map of $V$, or equation for $V$ of ...]