Reading: Chapters 35, 36, INTERFERENCE and DIFFRACTION
Study guide: Chapter 35
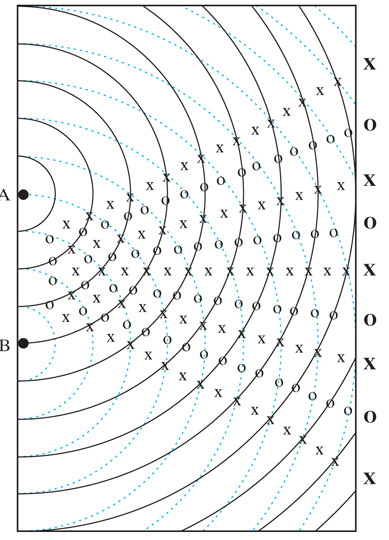 We
can pictorially calculate how this pattern should come out by marking up a diagram
of the undisturbed waves from the two sources with
We
can pictorially calculate how this pattern should come out by marking up a diagram
of the undisturbed waves from the two sources with
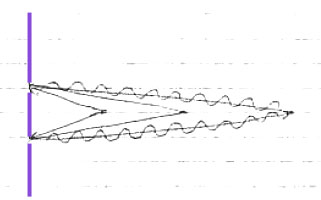
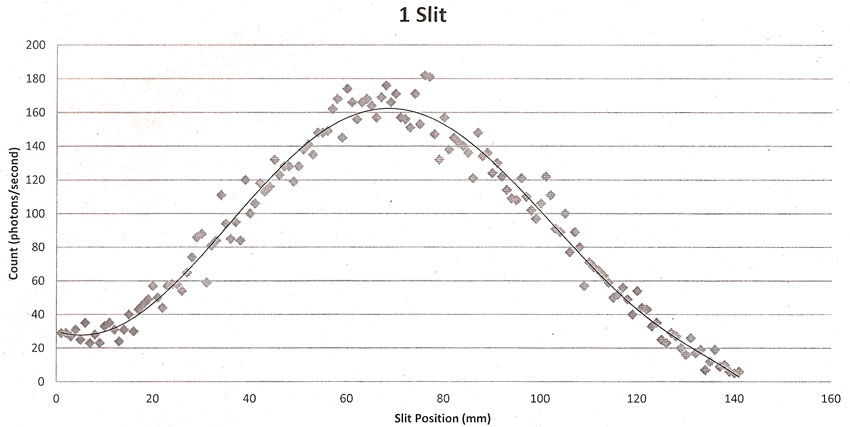
Have the waves from just one source hit a screen with two openings in it. Each opening acts like a "source" in its own right. But now the two "sources" are always in synch with each other, and are guaranteed to have the same frequency (that of the original plane wave coming at the wall).
If $d$ is the distance between $A$ and $B$, and $\Delta theta$ is the angular separation between the lines of constructive interference, it appears that
$$\Delta \theta \propto \frac{1}{d}$$.
Switching from wavefronts to rays...

Consider different directions ($\theta$) from the
two slits towards a distant screen...
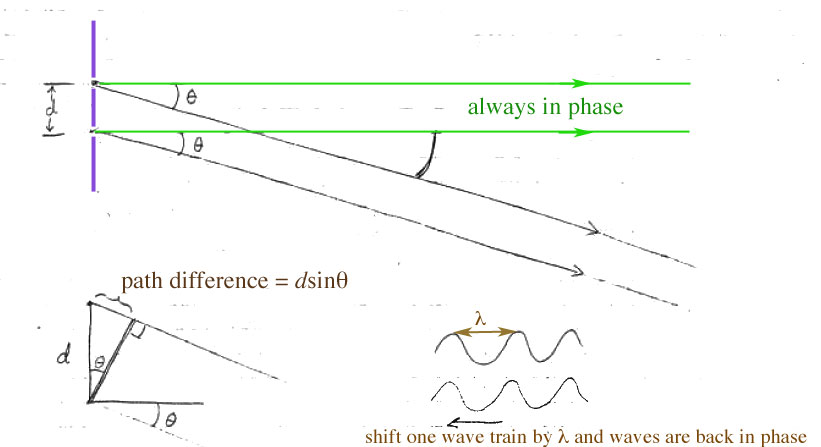
Waves from the two slits in the straight-ahead $\theta=0$ direction are always in-phase.
In another direction $\theta$, a wavefront from the top source travels a distance $d\sin\theta$ longer than the other. If this difference is an integer, $m$, number of wavelengths, then the two 'rays' interfere constructively: $$m\lambda=d\sin\theta$$ $\Rightarrow $ maxima whenever $$\sin\theta=m\frac{\lambda}{d}$$
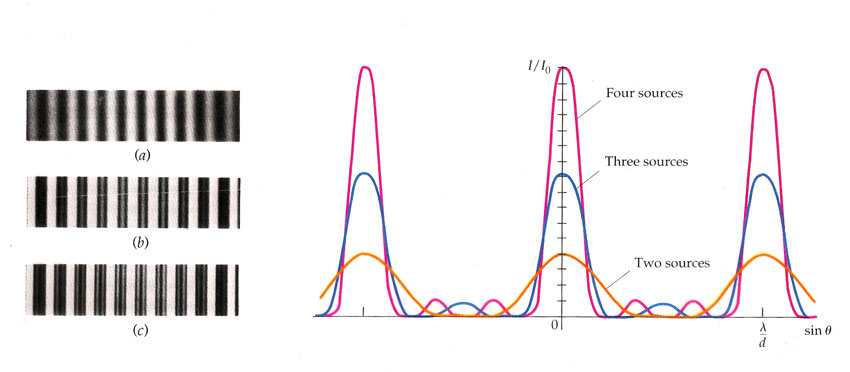
So if $\lambda\ll d$, then the angular separation between maxima is approximately:$$\Delta \theta\approx\frac{\lambda}{d}.$$
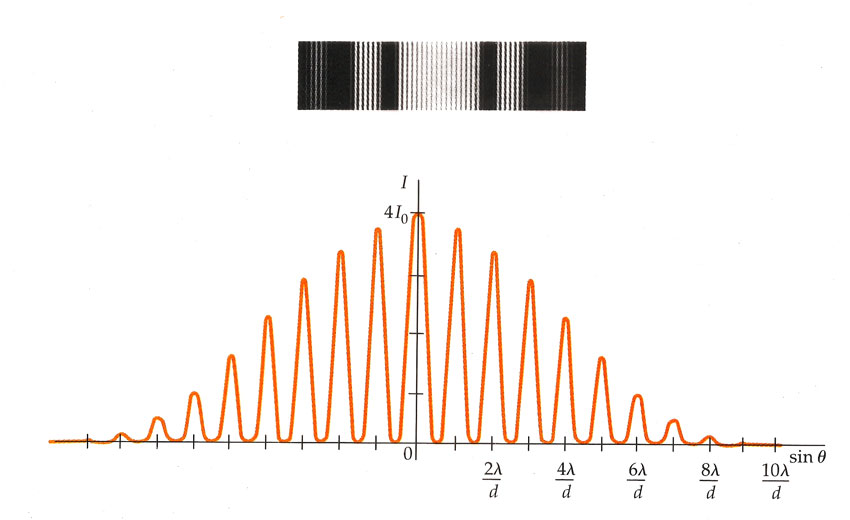
Pretty much like....
[Petey, Jacob, Tek]
Probably of finding one photon, $P_1$, in the apparatus at any one time *should have been* (time of flight of one photon)/(average time between counts):
Time of flight=0.5m/c=0.5m/3e8 m/s=1.7e-9 s
average time between counts $\approx$ 1 sec/ 400 counts = 0.0025 s
So $P_1\aprox6.8e-7 = 7\times 10^{-5}$%.
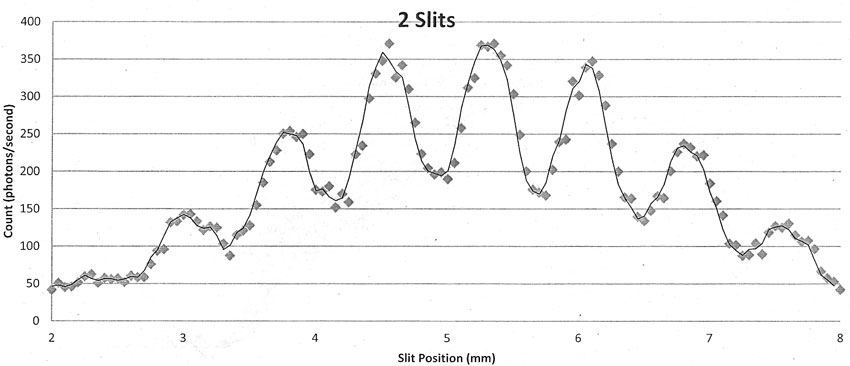
Single-slit:
Is this shape also a diffraction effect?
At what angle will we get destructive
interference?
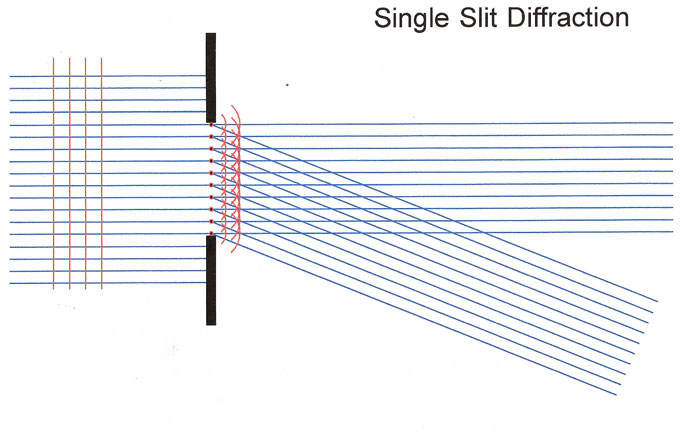
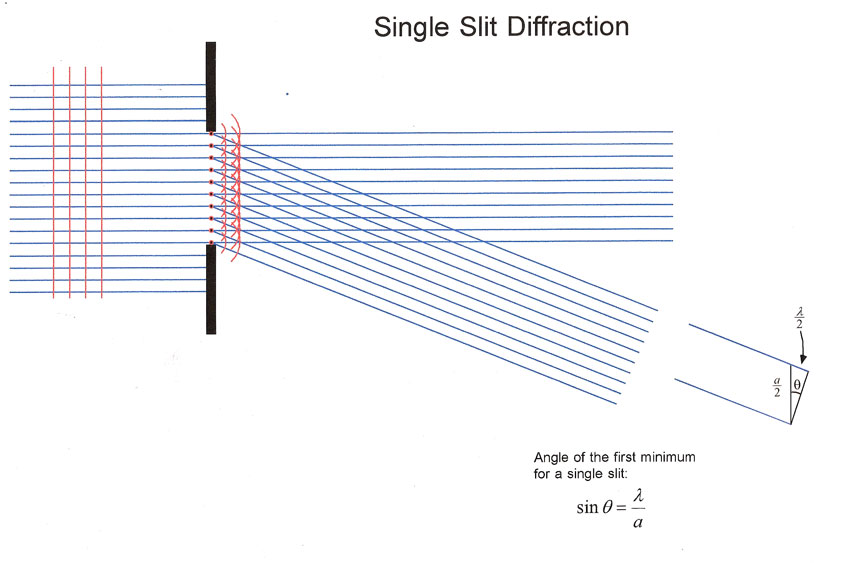
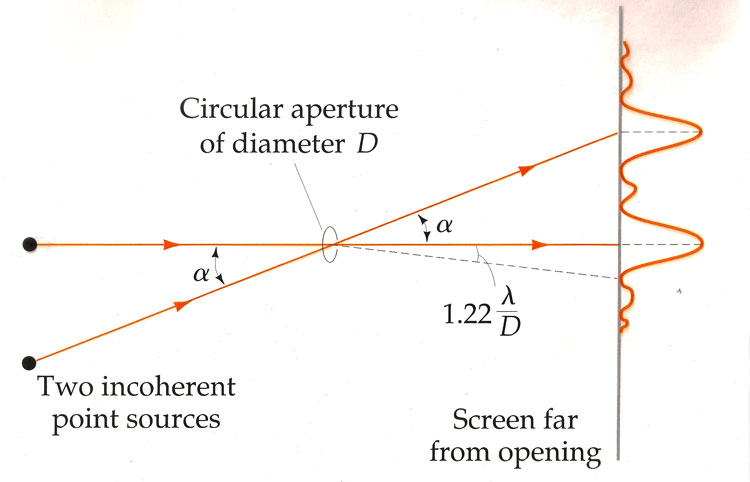
 Photo image of two sources...
Photo image of two sources...
a) $\alpha \gt 1.22\lambda/D$,
b) $\alpha \approx 1.22\lambda/D$.
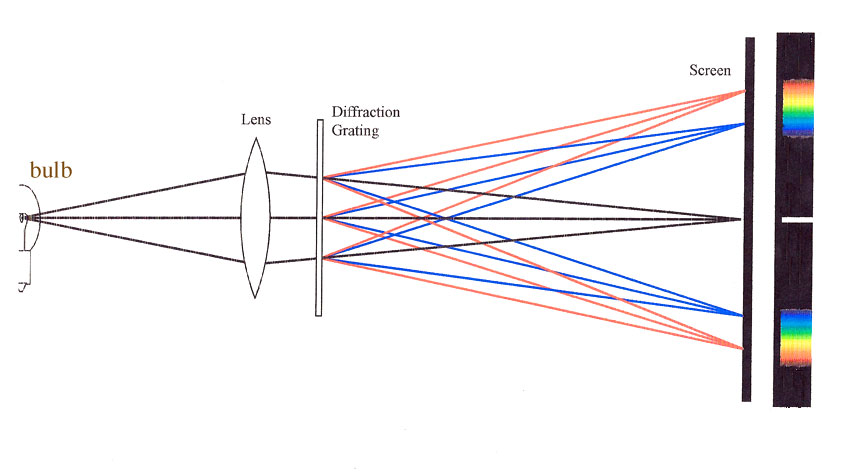
Diffraction grating
Used for separating colors (spectrometer)
Path difference for reflection from adjacent rows
of atoms separated by distance $d$ in terms of $\lambda$ of x-ray source is
$2d\sin\theta$, so constructive interference happens when this is an integer
number of wavelengths:$$m\lambda=2d\sin\theta$$.
There is a formula for the angular distance $\Delta \theta$ between destructive interference lines, (or between constructive interference lines, for that matter) in terms of the distance $d$ between the two slits (holes in the wall) which is:
$$\lambda=2d\sin\Delta\theta$$
The wavelength of the waves, $\lambda$ is a constant for what you've been looking at. Is this formula compatible with what you observed?
Initial parameters:
$ 0 189 10 2 true false 8 25 477 1 s 20 21 s 208 21 c 13833 0 w 16 0 l 29 w 61 0 l 111 w 13 0 c 15 0 w 20 0 l 10 c 59 0 l 1 w 30 0 l 62 w 5 0 l 10 w 7 0 c 43 0 l 2 w 4 0 l 5 c 139 0 w 14 0 c 5 0 w 6 0 l 4 c 152 0 w 48 0 c 37737 0