[4.4, 4.5] Compound interest
Compound interest
An account that pays a nominal interest rate of 12%, can be compounded...
- Annually: once per year interest on the Principal, $P$, is paid. At the end of the year, the balance in the account is: $$B=P+0.12P=(1.12)P$$
- Quarterly: Each quarter (3-months) interest of 12%/4=3% is added to the account. At the end of the year, the balance will be: $$B=(1.03)(1.03)(1.03)(1.03)P = (1.03)^4 P = 1.126 P$$ So, the effective annual rate of interest is 12.6%.
- Monthly, 12% compounded monthly means that every month 12%/12=1% is added to account. At the end of the year, the balance will be: $$B=(1.01)^{12} P= 1.127 P$$ So, the effective annual rate of interest is 12.7%
- Weekly,
- etc
Example
A $100 investment has a nominal annual interest rate of 20%.
- If interest is compounded annually, how much is the investment worth after one year?
- If interest is compounded semi-annually, how much is the investment worth after one year?
- If interest is compounded monthly, how much is the investment worth after one year?
- If interest is compounded daily, how much is the investment worth after one year?
If $n$ is the number of times per year that interest is paid, and $r$ is the nominal interest rate, and the principal amount is $P$, then the interest rate paid at the end of each period is $r/n$, and the the investment is worth a balance, $B$, of $$B(\text{one year})=P(1+r/n)^n$$ at the end of the year.
Generalizing to any time. If $t$ is the time in years, $r$ is the nominal interest rate, and $n$ is the number of times interest is compounded per year,
$$B(t)=P[(1+r/n)^n]^t=P(1+r/n)^{nt}$$
Continuous compounding
Is there a limit to this compounding in ever smaller intervals, or does money grow to infinite if you did that?
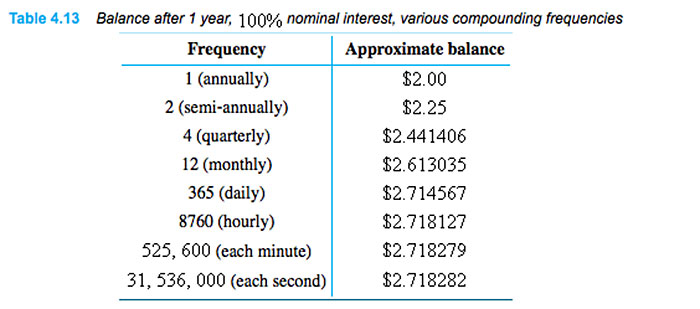
This is Euler's constant, "$e$", which is an irrational number: $e=2.71828182846...$
In this case, our interest rate was 100%, which is the same as a fractional growth rate of $r=1$. We can write the amount at the end of the year as: $$B=Pe=Pe^1.$$
So, perhaps this general formula for continuously compounding interest at a "nominal" rate $r$ looks plausible:
With continuous compounding, at a nominal rate $r$, the balance on an investment $P$ is worth this much at the end of one year: $$B(1)=Pe^r$$ and in general, after $t$ years is worth $$B(t)=P(e^{r})^t=Pe^{rt}.$$
4.5, question 3
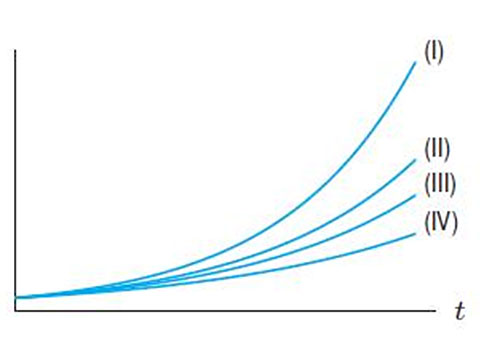
(even without a calculator) which of these functions matches which graph?
- $f(t)=e^{t/3}$
- $f(t)=(1.3)^t$
- $f(t)=e^{0.25 t}$
- $f(t)=(1.25)^t$
Euler's constant, $e$ is an irrational number: $e=2.71828182846...$
Inverse functions - graphically
For this table of of values of a function $f(x)$:

- Find $f^{-1}$. Graph $f(x)$ and $f^{-1}(x)$ on the same pair of axes.
- Suppose $h(x)=-3x+6$. Find $h^{-1}$. Graph $h(x)$ and $h^{-1}(x)$ on the same pair of axes.
Examples 3 & 4

- Let $g$ be defined by the graph. Graph $g^{-1}(x)$.
- Let $s(x)=x^2$. Find $s^{-1}$. Graph $s(x)$ and $s^{-1}(x)$ on the same pair of axes.